Revisiting Small Batch Training for Deep Neural Networks

The team at Graphcore Research has recently been considering mini-batch stochastic gradient optimization of modern deep network architectures, comparing the test performance for different batch sizes. Our experiments show that small batch sizes produce the best results.

We have found that increasing the batch size progressively reduces the range of learning rates that provide stable convergence and acceptable test performance. Smaller batch sizes also provide more up-to-date gradient calculations, which give more stable and reliable training. The best performance has been consistently obtained for mini-batch sizes between 2 and 32. This contrasts with recent work, which is motivated by trying to induce more data parallelism to reduce training time on today’s hardware. These approaches often use mini-batch sizes in the thousands.

The training of modern deep neural networks is based on mini-batch Stochastic Gradient Descent (SGD) optimization, where each weight update relies on a small subset of training examples. The recent drive to employ progressively larger batch sizes is motivated by the desire to improve the parallelism of SGD, both to increase the efficiency on today's processors and to allow distributed implementation across a larger number of physical processors. On the other hand, the use of small batch sizes has been shown to improve generalization performance and optimization convergence (LeCun et al., 2012; Keskar et al., 2016) and requires a significantly smaller memory footprint, but needs a different type of processor to sustain full speed training.

We have investigated the training dynamics and generalization performance of small batch training for different scenarios. The main contributions of our work are the following:

• We have produced an extensive set of experimental results which highlight that using small batch sizes significantly improves training stability. This results in a wider range of learning rates that provide stable convergence, while using larger batch sizes often reduces the usable range to the point that the optimal learning rate could not be used.
• The results confirm that using small batch sizes achieves the best generalization performance, for a given computation cost. In all cases, the best results have been obtained with batch sizes of 32 or smaller. Often mini-batch sizes as small as 2 or 4 deliver optimal results.

Our results show that a new type of processor which is able to efficiently work on small mini-batch sizes will yield better neural network models, and faster.

Stochastic Gradient Optimization

The SGD optimization updates the network parameters $\boldsymbol{\theta}$ by computing the gradient of the loss $L(\boldsymbol{\theta})$ for a mini-batch $\mathcal{B}$ of $m$ training examples, resulting in the weight update rule

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_k - \eta \; \frac{1}{m} \sum_{i=1}^{m} \nabla_{\boldsymbol{\theta}} L_i(\boldsymbol{\theta}_k) \, ,$$

where $\eta \;$ denotes the learning rate.

For a given batch size $m$ the expected value of the weight update per training example (i.e., per gradient calculation $\nabla_{\boldsymbol{\theta}} L_i(\boldsymbol{\theta})$) is proportional to $\eta/m$. This implies that a linear increase of the learning rate $\eta$ with the batch size $m$ is required to keep the mean weight update per training example constant.

This is achieved by the linear scaling rule, which has been recently widely adopted (e.g., Goyal et al., 2017).  Here we suggest that, as discussed by Wilson & Martinez (2003), it is clearer to define the SGD parameter update rule in terms of a fixed base learning rate $\tilde{\eta} = \eta / m$, which corresponds to using the sum instead of the average of the local gradients

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_k - \tilde{\eta} \; \sum_{i=1}^{m} \nabla_{\boldsymbol{\theta}} L_i(\boldsymbol{\theta}_k) \, .$$

In this case, if the batch size $m$ is increased, the mean SGD weight update per training example is kept constant by simply maintaining a constant learning rate $\tilde{\eta}$.

At the same time, the variance of the parameter update scales linearly with the quantity $\eta^2/m = \tilde{\eta} ^2 \cdot m \, $ (Hoffer et al., 2017). Therefore, keeping the base learning rate $\tilde{\eta}$ constant implies a linear increase of the variance with the batch size $m$.

Benefits of Small Batch Training

When comparing the SGD update for a batch size $m$ with the update for a larger batch size $n \cdot m$, the crucial difference is that with the larger batch size all the $n \cdot m$ gradient calculations are performed with respect to the original point $\boldsymbol{\theta}_k$ in the parameter space. As shown in the figure below, for a small batch size $m$, for the same computation cost, the gradients for $n$ consecutive update steps are instead calculated with respect to new points $\boldsymbol{\theta}_{k+j}$, for $j = 1, ..., n - 1$.

Therefore, under the assumption of constant base learning rate $\tilde{\eta}$, large batch training can be considered to be an approximation of small batch methods that trades increased parallelism for stale gradients (Wilson & Martinez ,2003).

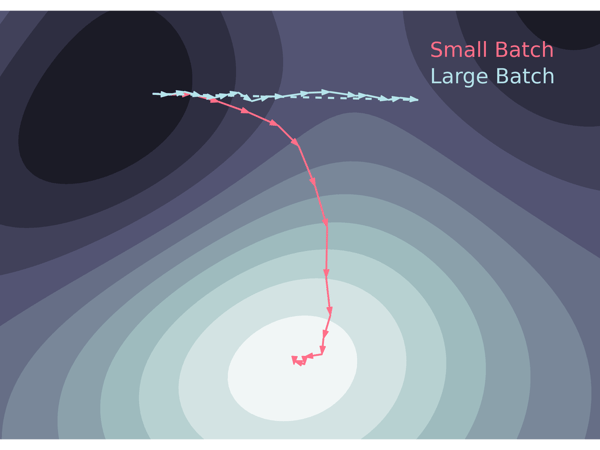
Small Batch sizes provide a better optimisation path

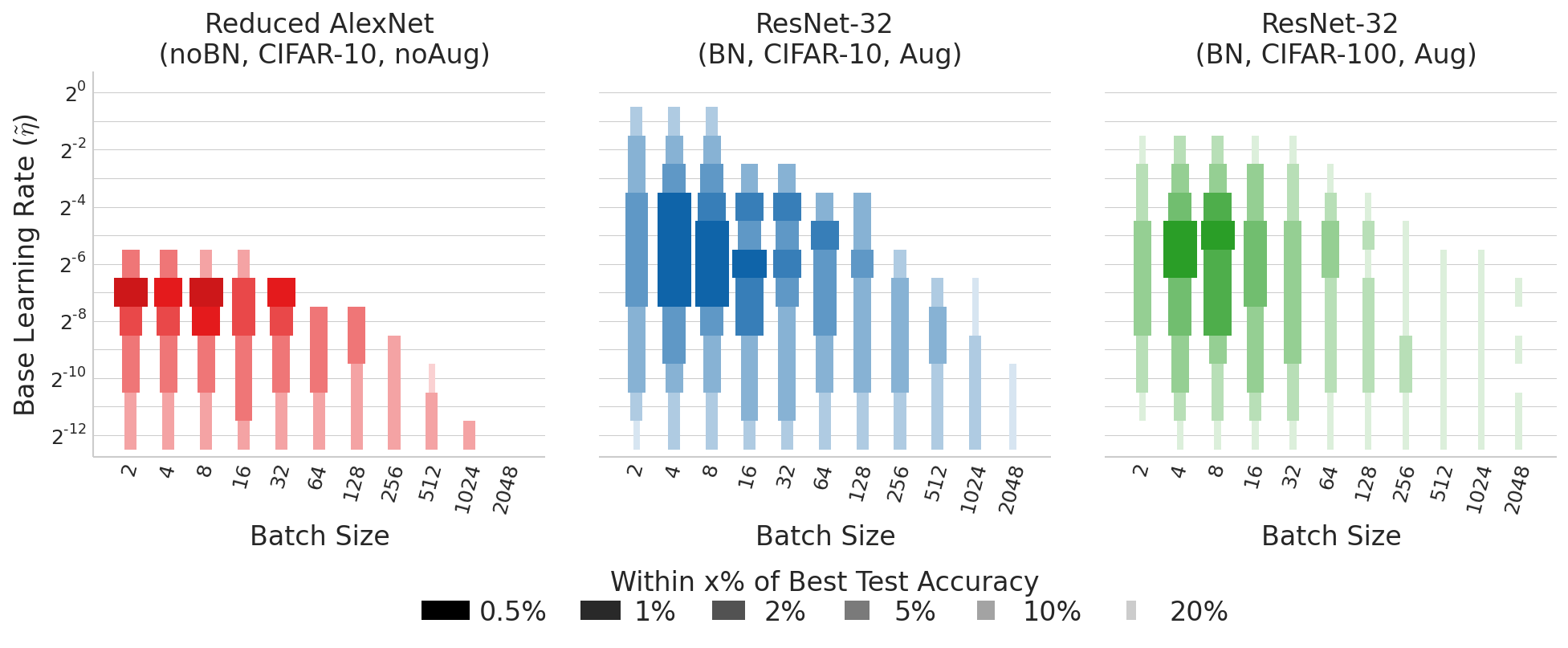
The CIFAR-10 test performance obtained for a reduced AlexNet model over a fixed number of epochs shows that using smaller batches gives a clear performance advantage. For the same base learning rate $\tilde{\eta}$, reducing the batch size delivers improved test accuracy. Also, using smaller batches corresponds to the largest range of learning rates that provide stable convergence.

Modern deep networks commonly employ Batch Normalization (Ioffe & Szegedy, 2015), which has been shown to significantly improve training performance. With Batch Normalization, each layer is normalized based on the estimate of the mean and variance from a batch of examples for the activation of one feature. The performance with Batch Normalization for very small batch size is typically affected by the reduced sample size available for estimation of the batch mean and variance. However, the collected data shows best performance with batch sizes smaller than previously reported.

The following figure shows the CIFAR-100 performance for ResNet-32, with Batch Normalization, for different values of batch size $m$ and base learning rate $\tilde{\eta}$. The results show again a significant performance degradation for increasing values of the batch size, with the best results obtained or batch sizes $m = 4$ or $m = 8$. The results also indicate a clear optimum value of base learning rate, which is only achievable for batch sizes $m=8$ or smaller.

As summarized in the following figure, increasing the batch size progressively reduces the range of learning rates that provide stable convergence. This demonstrates how the increased variance in the weight update associated with the use of larger batch sizes can affect the robustness and stability of training. The results clearly indicate that small batches are required to achieve both the best test performance, and allow easier and more robust optimization.

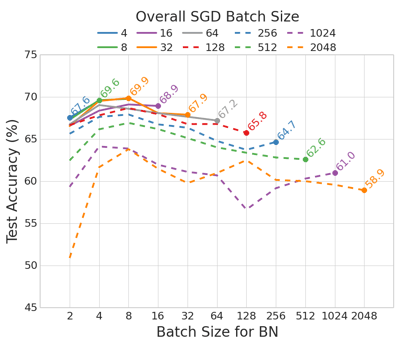
Different Batch Sizes for Weight Update and Batch Normalization

In the following figure, we consider the effect of using small sub-batches for Batch Normalization, and larger batches for SGD. This is common practice for the case of data-parallel distributed processing, where Batch Normalization is often implemented independently on each individual processor, while the gradients for the SGD weight updates are aggregated across all workers.

The CIFAR-100 results show a general performance improvement by reducing the overall batch size for the SGD weight updates. We note that the best test accuracy for a given overall SGD batch size is consistently obtained when even smaller batches are used for Batch Normalization. This evidence suggests that to achieve the best performance both a modest overall batch size for SGD and a small batch size for Batch Normalization are required.

Why it matters

Using small batch sizes has been seen to achieve the best training stability and generalization performance, for a given computational cost, across a wide range of experiments. The results also highlight the optimization difficulties associated with large batch sizes. Overall, the experimental results support the broad conclusion that using small batch sizes for training provides benefits both in terms of the range of learning rates that provide stable convergence and the test performance for a given number of epochs.

While we are not the first to conclude that smaller mini-batch sizes give better generalization performance, current practice is geared to ever larger batch sizes because today's hardware requires a trade-off between getting more accurate results and synthesizing parallelism to fill the wide vector data-paths of today's processors, and to hide their long latencies to model data stored off-chip in DRAM.

With the arrival of new hardware specifically designed for machine intelligence, like Graphcore’s Intelligence Processing Unit (IPU), it’s time to rethink conventional wisdom on optimal batch size. With the IPU you will be able to run training efficiently even with small batches, and hence achieve both increased accuracy and faster training. In addition, because the IPU holds the entire model inside the processor, you gain an additional speed up by virtue of not having to access external memory continuously. Our benchmark performance results highlight the faster training times that can be achieved.

You can read the full paper here https://arxiv.org/abs/1804.07612.