계량경제학 모델은 데이터 기반 금융 기관에서 중추 역할을 합니다. 이 모델을 사용하면 경제 현상을 통계적인 방법으로 모델링하여 정보에 입각한 의사결정을 내릴 수 있습니다.
영국 런던에 본사를 둔 투자 관리사 맨 그룹(Man Group)은 CRR(Cox-Ross-Rubinstein)과 같은 옵션 가격 결정 모델을 사용하여 매일 수백만 옵션의 가치를 평가합니다. 맨 그룹에서 정량적 연구를 수행하는 연구진은 경쟁우위를 확보하고자 이러한 모델의 성능 개선을 위해 지속적으로 노력하고 있는데요, 최근 IPU를 활용한 인상적인 결과를 얻었습니다.
발라즈 도몽코스(Balazs Domonkos) 맨 그룹의 알파 테크놀로지 부문 수석 엔지니어는 “옵션 가격 결정은 중요한 워크로드로, 연산이 매우 까다롭다. CRR 알고리즘은 지금까지도 IPU로 옵션 가격 결정을 테스트하기 좋은 벤치마크”라며, “최근 그래프코어와 함께 수행한 연구에서 IPU가 CPU보다 최대 21배 빠르게 가격 결정 워크로드를 수행하며 IPU만의 대규모 병렬처리 특성을 입증했다”고 전했습니다.
CPU는 쉽게 벡터화할 수 없는 계량경제학 워크로드를 처리하는 유연성 덕분에 여전히 많은 금융 기관에서 GPU보다 선호되고 있습니다. IPU는 CPU와 동일한 MIMD 유연성을 제공하는 동시에, 훨씬 더 높은 플롭스 성능과 처리 속도를 구현하기 때문에 이러한 워크로드를 가속화할 수 있습니다. 따라서, CPU의 훌륭한 대안이 될 수 있는데요. 이러한 범주에 해당하는 벡터화하기 어려운 세 가지 유형의 워크로드는 다음과 같습니다.
조건부 종료(termination) 워크로드: 이러한 워크로드에는 조건이 충족되거나 입력에 따라 결정되는 특정 반복 횟수가 완료될 때까지 지속되는 루프가 포함됩니다. 배치 처리를 사용하는 경우 모든 샘플이 완료되어야 배치가 완료된 것으로 간주됩니다. 자동 호출 이벤트가 트리거되면 종료될 수 있는 자동 호출 옵션 가격 결정 모델을 예로 들 수 있습니다.
순차적 워크로드: 여기에는 반복적이고, 루프를 기반으로 하며, 재귀적인 워크로드가 포함될 수 있습니다. 여러 번 실행할 필요가 없는 순차 워크로드의 경우 현재 연산의 출력이 다음 연산에 대한 입력으로 필요하기 때문에 벡터화할 수 없습니다. 해밀턴 역학을 반복적으로 시뮬레이션하는 해밀턴 몬테 카를로(Hamiltonian Monte Carlo)를 그 예로 볼 수 있습니다.
입력 종속 라우팅 워크로드: 이러한 모델로는 트리 기반 모델 및 조건문(if-문)을 사용하는 기타 형태의 모델이 있습니다. 배치의 각 요소에 대해 수행된 작업이 분산될 경우 이러한 워크로드를 벡터화하기 어려울 수 있습니다. 깊이(depth)가 가변적인 의사결정 트리가 좋은 예로 할 수 있습니다.
이번 포스팅에서는 이러한 알고리즘 중 하나인 이항 옵션 가격 결정 모델을 살펴볼텐데요, 이 모델은 흔히 CRR모델로 잘 알려져 있습니다. CRR은 미국식 옵션 보유자가 언제든지 옵션을 행사할 있는 권리 등 광범위한 조건을 처리하는 유연성 때문에 옵션 가격 결정에 널리 활용되고 있습니다. 이제부터 CRR 모델의 작동 방식, 벡터화에 따르는 몇 가지 단점, 그리고 IPU에서 이를 대규모로 실행하는 방법에 대해 알아보겠습니다.
CRR 모델을 사용한 가격 결정 옵션
CRR모델은 평가일과 만료일 사이에 시뮬레이션된 여러 개별적 시간 단계(n)에서 자산의 가격이 어떻게 변동할 수 있는지를 고려하여 옵션의 가격을 책정합니다. 시뮬레이션된 시간 단계 수가 많을수록 가격 결정이 더 정확해집니다.
이 모델은 2가지 단계로 구성되는데요. 정방향 예측(forward pass)으로 알려진 1단계에서는 기초자산 가격이 각 시뮬레이션 시간 단계에 따라 현재 현물 가격인 S0에서 특정 계수(u 또는 d)만큼 증가하거나 감소한다고 가정하여 가격 트리를 생성합니다. 자산이 증가하거나 감소할 수 있는 계수는 자산의 변동성과 시뮬레이션된 시간 단계의 크기 간의 상관관계에 따라 계산됩니다.
역방향 예측(backward pass)으로 알려진 2단계에서는 옵션의 가치가 가격 트리의 뒤로 이동함으로써 반복적으로 계산됩니다. 각 시간 단계에서 이전 시점의 옵션 가치는 기초자산이 증가하거나 감소했을 확률을 고려하여 계산됩니다. 이를 이항 값이라고 합니다.
이항식 매개변수 p는 특정 시뮬레이션 시점에서 가격이 상승할 확률을 나타냅니다. p는 대표하는 이항 분포가 측정된 변동성과 가정된 할인율로 자산의 브라운 운동을 시뮬레이션하도록 설정됩니다.
유럽식 옵션과 미국식 옵션에서 실행되는 각각의 경우에서 알고리즘의 역방향 예측에 차이가 발생한다는 점을 유의해야 합니다. 이러한 차이는 언제든 옵션을 행사할 수 있는 미국식 옵션 보유자의 권리를 반영하는 조건을 실행하여 CRR 알고리즘의 유연성을 활용합니다.
벡터화의 부작용
CRR 알고리즘의 강점은 사용자가 어느 시간 단계에서든지 조건을 추가할 수 있다는 점에 있습니다. 미국식 옵션 가격 결정에는 옵션의 가치가 즉시 옵션을 즉시 행사하여 얻을 수 있는 가치보다 낮을 수 없다는 조건이 추가됩니다.
이러한 조건에도 불구하고 CRR 알고리즘을 트리 높이와 옵션 배치 모두에서 벡터화할 수 있습니다. 이러한 실행 사례는 Google의 tf-quant 금융 라이브러리인 tf-quant-finance/crr_binomial_tree에서 찾을 수 있습니다. 여기서는 미국식 옵션과 유럽식 옵션의 혼합 배치 전반에서 알고리즘을 벡터화합니다. 따라서 배치의 각 입력이 미국식 옵션인지 유럽식 옵션인지에 관계없이 동일한 연산을 수행해야 합니다.
유럽식 옵션은 옵션을 즉시 행사하도록 요구하기 때문에 더 높은 수익을 달성할 수 있는지 계산할 필요가 없어 처리에 필요한 연산 수가 미국식 옵션보다 적어야 합니다. 하지만 이러한 형태의 벡터화는 미국식 옵션과 유럽식 옵션의 가격 결정에 동일한 연산을 실행하도록 요구하기 때문에 처리량은 두 옵션 사이에서 동일합니다. 아래 그림 1에서 이 과정을 확인할 수 있습니다.
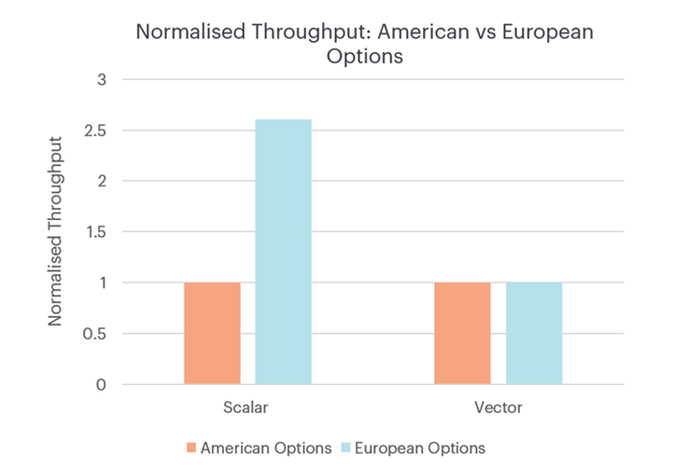
스칼라 워크로드로 실행하는 경우 유럽식 옵션의 가격 책정(파란색)이 미국식 옵션의 가격 결정(주황색)보다 훨씬 빠릅니다. 처리량은 미국식 옵션의 처리량으로 정규화됩니다.
CRR의 경우 유럽식 옵션과 미국식 옵션을 위한 두 개의 코드 복사본을 유지하여 'if' 문을 제거하는 방식으로 큰 어려움 없이 문제를 해결할 수 있습니다. 하지만 CRR 및 기타 계량 경제학 모델의 변형에서는 수정이 그리 간단하지 않습니다.
벡터화된 실행이 아닌 스칼라를 사용하는 또 다른 이유는 데이터 지역성을 적용한다는 것입니다. 벡터화된 연산으로 배치를 처리할 때는 후속 연산에 대비하여 컴퓨팅 코어와 캐시 간에 데이터가 교환될 가능성이 높습니다. 스칼라 실행에서는 코어/스레드 간에 상호 의존성이 없기 때문에 이 문제를 방지할 수 있습니다.
단일 IPU에서 병렬로 8,832개 옵션의 가격을 책정하는 IPU의 MIMD 아키텍처
CPU 및 그래프코어 IPU와 같이 MIMD 프로세서는 SIMD 프로세서(GPU)보다 더 높은 유연성을 제공합니다. IPU를 사용하면 스레드는 다른 스레드에서 수행하는 작업에 관계없이 모든 명령을 실행할 수 있는 반면, GPU에서는 각 스레드가 동일한 명령을 실행해야 하므로 벡터화가 필요합니다.
IPU 프로세서의 스칼라 연산을 사용하면 입력 종속 라우팅을 수용하는 것이 간단합니다. 샘플 배치를 연산하는 대신 각 샘플이 해당 샘플에 필요한 컴퓨팅 경로를 자유롭게 실행할 수 있는 단일 스레드로 배포됩니다. 따라서 샘플이 수렴되면 처리가 중단되고 스레드가 제어 프로그램으로 반환됩니다. 해당 샘플의 속성 때문에 프로그램에서 특정 코드 섹션(if 문)을 실행할 필요가 없는 경우 자유롭게 건너뜁니다. GPU의 배치 처리에서는 이러한 세밀한 제어가 불가능합니다.
하드웨어를 작업자 풀로 간주하고, 독립적인 처리를 위해 각 작업자에게 옵션을 배포함으로써 IPU 프로그래밍 모델에서 대량의 옵션 가격 책정을 쉽게 처리할 수 있습니다. 작업자가 처리를 완료하면 제어 프로그램으로 돌아가 다른 옵션과 함께 다시 배포할 수 있습니다. 이 프로세스는 CPU에서와 마찬가지로 IPU에서도 유사하게 작동합니다.
CPU와 달리 IPU는 1,472개 타일과 8,832개 병렬 스레드를 갖는 대규모 병렬 MIMD 칩으로, 다른 모든 스레드와 독립적으로 작동할 수 있습니다. 따라서 CPU와 마찬가지로 성능 개선을 얻기 위해 벡터화된 프로그램에 의존할 필요가 없으며, 오늘날 가장 큰 서버급 CPU보다 2배 더 많은 코어를 가지고 있습니다.
단일 옵션을 단일 프로세서 스레드에 매핑하면(IPU는 IPU 타일당 6개 스레드 보유) 단일 IPU에서 병렬로 8,832개 옵션의 가격을 책정할 수 있습니다. 아래는 24개 코어로(2배 하이퍼스레딩으로 스레드는 48개) 48개 옵션 가격을 병렬로 책정할 수 있는 표준 서버급 CPU와의 비교입니다. 단일 MK2 IPU 및 단일 CPU(Intel Xeon Platinum 8168) 간 처리량 비교는 그림 2에서 확인할 수 있습니다.
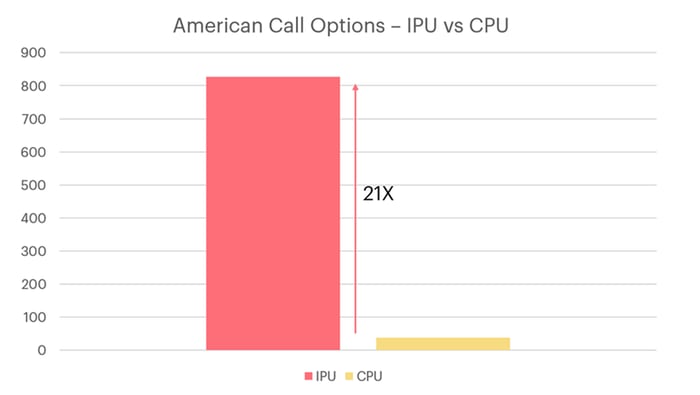
IPU는 CRR 알고리즘을 사용하여 미국식 옵션의 가격을 책정하는 경우 서버급 CPU보다 최대 21배 높은 처리량을 제공합니다.
IPU가 제공하는 병렬 처리가 CRR 알고리즘이 IPU에서 효과적으로 실행되는 유일한 이유는 아닙니다. CPU는 약 10GB/s의 읽기/쓰기 속도(메모리 계층 구조를 사용해 약간 개선될 수 있음)로 액세스할 수 있는 오프칩 DRAM에 가격 트리를 저장합니다. 하지만 IPU는 전체 가격 트리를 47TB/s의 읽기/쓰기 속도로 액세스할 수 있는 900MB의 인프로세서 메모리에 명시적으로 저장합니다.
CRR 알고리즘은 입력 종속 라우팅을 사용하는 워크로드의 한 가지 예로, 이 워크로드의 일반적인 벡터화에는 가능한 가장 긴 컴퓨팅 경로의 속도로 실행된다는 단점이 따른다는 것이 입증되었습니다.
결론
CPU는 쉽게 벡터화할 수 없는 워크로드를 처리하는 유연성으로 여전히 많은 금융 기관에서 사용되고 있습니다. 하지만 그래프코어 IPU는 CPU와 동일한 MIMD 유연성을 제공하는 동시에, 플롭스 성능과 처리 속도가 훨씬 더 높기 때문에 이러한 워크로드를 가속화할 수 있습니다.
