Probabilistic Modelling by Combining MCMC and Variational Inference with IPUs

MCMC is iterative, making it inefficient on most current hardware geared towards highly structured, feed-forward operations. In contrast, the IPU can support probabilistic machine learning algorithms like MCMC which reflect the level of noise in the data, and therefore the uncertainty of their predictions. Here we explore IPU acceleration of such algorithms, and the research breakthroughs this might produce.

There is no doubt that the advances of deep learning in recent years are impressive. However, most commonly used deep networks have a fundamental limitation: they do not internalise uncertainty. Given an input, they produce only a point estimate of the output, with no indication of the level of confidence. Probabilistic machine learning aims to build models of the world in which an estimation of the noise is inherent; models which have an idea of what they don’t know.

Let’s make this more concrete. Consider autonomous driving with a model-based Reinforcement Learning (RL) setup. We have a model of the world which forecasts how the surroundings will play out in the near future, and an agent which chooses an action (acceleration, direction, etc.) based on the model’s predictions. Clearly, a deterministic model that predicts only one future is less informative than one that predicts a distribution over many futures. In the first case, a pedestrian may be forecasted to walk into the road, or not. However, the prediction model is imperfect, and choosing the action based on the predicted future could be extremely risky. Suppose instead that we have a probabilistic model that predicts a distribution over futures. Such a model's predictions come with an indication of uncertainty that, for example, the pedestrian walks into the road. This uncertainty estimation allows the agent to plan conservatively in these types of applications, and hopefully avoid undesirable outcomes.

Two commonly used approaches to probabilistic inference are Markov Chain Monte Carlo (MCMC) and Variational Inference (VI). Both seek to circumvent intractable integrals needed to calculate the distribution of interest, but do so in different ways. MCMC uses iterative sampling of an implicit distribution with schemes such as Hamiltonian Monte Carlo (HMC), Langevin dynamics, or Metropolis Hastings, whereas VI introduces an approximate distribution, which is then sampled and optimised to get as close as possible to the target. These two approaches are traditionally considered distinct, but some recent research has explored ways to combine them (see for example Salimans et al. (2014), Habib & Barber (2018), Hoffman (2017)).

In this post, we have looked at the Variational Autoencoder (VAE) model described in the paper A Contrastive Divergence for Combining Variational Inference and MCMC, by Ruiz and Titsias, presented at ICML earlier this year (Ruiz & Titsias (2019)). Their approach extends the Evidence Lower Bound (ELBO) objective, used to train a vanilla VAE, with their Variational Contrastive Divergence (VCD). In VCD, HMC improves the latent representation, and feeds back into the gradients used to update the encoder parameters.

The flow of data through the model is more involved than a standard VAE, though the first step is the same: the input is passed through the encoder, which estimates the mean and variance of the approximate posterior. A sample from the resulting Gaussian is then iteratively improved by HMC, guided by gradients of the decoder to move it closer to a sample from the true posterior. The parameter updates of the encoder are, in turn, improved with the HMC samples.

The resulting format of the gradient estimator contains a “score function” term, which can have high variance and thus make training less effective. To mitigate this, the authors employ control variates — additional variables which reduce the variance of the gradient without introducing bias. They begin the first 3000 training iterations with a global (scalar) control variate, after which they use local (vector) control variates, with a single value per training example.

The sequential nature of MCMC, and therefore the inability to vectorise along a single chain, presents challenges to existing hardware, as most accelerators extract efficiency from highly parallel computation of the same operation. Here we demonstrate the efficiency of the Graphcore IPU for sequential algorithms such as MCMC.

Based on the authors’ original Matlab code, we have implemented the model in TensorFlow and TensorFlow Probability, and have run it on IPU as well as a leading alternative processor. The standard TensorFlow API maps onto Poplar, our lower level computation-graph library, which is then compiled and executed on IPU. We compare our results on a single IPU against those achieved when running on the other hardware. Following the paper by Ruiz and Titsias, we train and evaluate the model on the statically binarised MNIST dataset (Salakhutdinov & Murray (2008)).

The implementation run on both devices is largely the same, in order to allow fair comparison. All experiments on the alternative hardware are run with multiple iterations inside a tf.while_loop() to reduce the overhead of the tf.Session.run(). We find this to run faster than executing a single iteration per session call.

Our experiments show that we can use a more memory-efficient scalar control variate throughout training with no discernible effect on the log-likelihood (see Train Faster), and that training the model with larger batch sizes can degrade the test set score (see Batch Sizes).

Train Faster

First, let’s check our experiment does what it should. Training for 16 runs, with the same hyperparameters as published in the ICML paper or Matlab implementation, we achieve the results given below. The intervals reported are one standard deviation either side of the mean.

*Projected based on 30,000 iterations

The authors report a single log-likelihood value: -95.86. Reassuringly, both sets of experiments we conducted have a mean test score consistent with (within a single standard deviation of) this result, and we’ve generated a speedup of 1.7x just by running on IPU. Again, there are no special IPU-optimisations in the TensorFlow used for the above experiments.

We then tested the effect of the control variate configuration. In the interest of scaling to large datasets, we would prefer to have a model in which the size of the variables is not in direct correspondence to the size of the training set. Thus we measure the effect of replacing the local control variates with a global control variate, which is used throughout training. We have run this configuration with IPU infeeds, where multiple training operations can be run in a single TensorFlow session call. This significantly reduces the fractional computational overhead of invoking the tf.Session.run(). Let’s see how a scalar control variate fares:

*Projected based on 30,000 iterations

This clearly speeds up training considerably. We are now more than 2x faster than using local control variates, and 4.1x faster on IPU at 150W compared to the alternative processor at 300W. All with no reduction in test set log-likelihood.

So where is this 4.1x speedup coming from? What does the IPU do differently? Most existing machine learning hardware platforms process simple arithmetic operations with large tensors very efficiently, which is good for highly structured feed-forward networks with large batches of data. However, we often want to train models with more elaborate structures. The VAE with Variational Contrastive Divergence is a good example. For this algorithm, the data is passed through an encoder before then doing multiple evaluations of the decoder, using its gradients to direct the HMC chain. The HMC is by nature recurrent, so we cannot parallelise along the chain. Indeed, if we take the TensorFlow Probability HMC implementation, we find that the IPU executes a single one_step() function of a unidimensional chain 15.1x faster than the alternative hardware accelerator.

It is true however that, for most accelerators, using a larger batch size can mitigate the reduced throughput. We will explore this in the next section.

Batch Sizes

In the experimental set up of the Ruiz and Titsias paper, the authors use a batch size of 100. We investigate the variation of performance for batch sizes 16, 128, 512 and 1024.

Using the final 10,000 examples from the training set for validation, we have carried out a learning rate sweep for each batch size. We then train with the optimal learning rate on the full training set. We train for 8,200 epochs, rather than 800 as described in the paper, and so we proportionally extend the learning rate decay schedule. The figure below illustrates the test set performance over 15 runs.

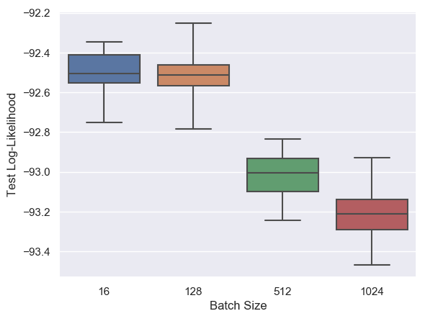
Notice first that we can achieve a significant boost in the test score above the published -95.86 simply by training for more epochs. This is an obvious benefit of hardware acceleration.

What do we conclude about batch sizes? Batch sizes 16 and 128 perform similarly, but using batch sizes larger than 128 significantly reduces the test log-likelihood. Therefore, while we might increase the batch size in order to boost the throughput, the test score suffers above a certain threshold.

Conclusion

We have taken a model which is, at present, challenging to most alternative processors and implemented it in TensorFlow. We have shown how, without any advanced software implementation, training can be sped up considerably using IPUs, enabling faster development and experimentation of algorithms previously poorly served by current hardware. While throughput with other processors can be increased with larger batch sizes, we have seen that this is detrimental to the asymptotic log-likelihood score.

The speedup observed here lowers the computational cost of using MCMC to improve VAEs in other applications. This might be for better generation quality of other media — text (Yang et al. (2017)), music (Roberts et al. (2018)) or handwriting  (Chung et al. (2015))— or superior latent representation learning. Better latent representations could admit better world models in model-based RL, allowing more effective planning or better policy learning in the latent space (see for example Hafner et al. (2019) and Ha & Schmidhuber (2018)). Such algorithms have a wide range of real-world applications such as robotics (as for example in Zhang et al. (2019)), self-driving cars (Wayve (2018)), and drone racing (Bonatti et al. (2019)).

Many other generative models use MCMC, and would benefit from better computational efficiency. For example, in the recent work on Energy-Based Models (Du & Mordatch (2019)), faster Langevin sampling would reduce the wall-clock time both in training and in generating samples from the trained model. Similarly, Gibbs sampling has been shown to improve the modelling of scores of music (Huang et al. (2019)), and could be significantly faster on IPU. Gibbs sampling is also commonly used in Topic Modelling (see for example Griffiths & Steyvers (2004)), a branch of NLP seeking to find a distribution of topics in a document, given the words it contains.

In addition to generative modelling and representation learning, there are also benefits of faster execution of MCMC in more direct applications. MCMC is applied in many contexts where closed-form integrals cannot be calculated. For example, in finance MCMC is used to estimate the prices of assets and how they evolve in time (Johannes & Polson (2003)), and how different elements of a portfolio contribute to its overall risk (Koike & Miname (2019)). In epidemiology, MCMC can be a valuable tool for better understanding diseases (Hamra et al. (2013)), and can be used for medical diagnosis of Alzheimer’s disease (Alexiou et al. (2017)) and blood cancer (Vaikundamoorthy (2017)). There are countless other domains in which the parameters of complex processes are inferred using MCMC: climate science (Solonen et al. (2012)), signal processing (Martino (2018)) and seismology (de Figueiredo (2019)) to name a few.

Graphcore Research identifies new directions of AI research that take advantage of our unique IPU architecture and which will contribute to discover ground-breaking approaches in machine intelligence. We have the freedom to experiment and pursue complex research challenges which we will publish so everyone can benefit from them. Please subscribe to our blog here to keep up to date on blogs, papers and other research work we undertake.

Alexiou, V.D. Mantzavinos, N.H. Greig and M.A. Kamal. “A Bayesian Model for the Prediction and Early Diagnosis of Alzheimer's Disease.” Front Aging Neurosci. 9:77. 2017.

Rogerio Bonatti, Ratnesh Madaan, Vibhav Vineet, Sebastian Scherer, and Ashish Kapoor. “Learning Controls Using Cross-Modal Representations: Bridging Simulation and Reality for Drone Racing.” arXiv preprint arXiv:1909.06993. 2019.

Junyoung Chung, Kyle Kastner, Laurent Dinh, Kratarth Goel, Aaron C. Courville, and Yoshua Bengio. “A recurrent latent variable model for sequential data.” Advances in neural information processing systems, pp. 2980-2988. 2015.

Yilun Du and Igor Mordatch. “Implicit generation and generalization in energy-based models.” arXiv preprint arXiv:1903.08689. 2019.

L.P. de Figueiredo, D. Grana, M. Roisenberg and B.B. Rodrigues. “Gaussian mixture Markov chain Monte Carlo method for linear seismic inversion.” Geophysics, 84(3), R463-R476. 2019.

Thomas L. Griffiths and Mark Steyvers. “Finding scientific topics.” Proceedings of the National academy of Sciences 101, no. suppl 1, pp. 5228-5235. 2004.

David Ha and Jürgen Schmidhuber. “Recurrent world models facilitate policy evolution.” Advances in Neural Information Processing Systems, pp. 2450-2462. 2018.

Raza Habib and David Barber. “Auxiliary Variational MCMC.” International Conference on Learning Representations. 2019.

Danijar Hafner, Timothy Lillicrap, Ian Fischer, Ruben Villegas, David Ha, Honglak Lee, and James Davidson. “Learning latent dynamics for planning from pixels.” arXiv preprint arXiv:1811.04551. 2018.

Matthew D. Hoffman. “Learning Deep Latent Gaussian Models with Markov Chain Monte Carlo.” International Conference on Machine Learning. 2017.

Cheng-Zhi Anna Huang, Tim Cooijmans, Adam Roberts, Aaron Courville, and Douglas Eck. “Counterpoint by convolution.” arXiv preprint arXiv:1903.07227. 2019.

Michael Johannes and Nicholas Polson. “MCMC methods for continuous-time financial econometrics.” In Handbook of Financial Econometrics: Applications, pp. 1-72. Elsevier, 2010.

Luca Martino. “A review of multiple try MCMC algorithms for signal processing.” Digital Signal Processing 75, pp 134-152. 2018.

Adam Roberts, Jesse Engel, Colin Raffel, Curtis Hawthorne and Douglas Eck. “A Hierarchical Latent Vector Model for Learning Long-Term Structure in Music.” International Conference on Machine Learning, pp. 4361-4370. 2018.

Francisco Ruiz and Michalis Titsias. “A Contrastive Divergence for Combining Variational Inference and MCMC.” International Conference on Machine Learning, 2019.

Ruslan Salakhutdinov and Iain Murray. "On the quantitative analysis of deep belief networks." International conference on Machine learning. 2008.

Tim Salimans, Diederik Kingma and Max Welling. “Markov Chain Monte Carlo and Variational Inference: Bridging the Gap.” International Conference on Machine Learning. 2015.

Antti Solonen, Pirkka Ollinaho, Marko Laine, Heikki Haario, Johanna Tamminen and Heikki Järvinen. “Efficient MCMC for Climate Model Parameter Estimation: Parallel Adaptive Chains and Early Rejection.” Bayesian Anal. 7. no. 3, pp. 715-736. 2012.

Koike Takaaki and Mihoko Minami. “Estimation of risk contributions with MCMC.” Quantitative Finance, 19:9, pp. 1579-1597. 2019.

Wayve AI, “Dreaming About Driving.” 2018.

Zichao Yang, Zhiting Hu, Ruslan Salakhutdinov and Taylor Berg-Kirkpatrick. “Improved variational autoencoders for text modeling using dilated convolutions.” International Conference on Machine Learning, pp. 3881-3890. 2017.

Marvin Zhang, Sharad Vikram, Laura Smith, Pieter Abbeel, Matthew Johnson, and Sergey Levine. “SOLAR: Deep Structured Representations for Model-Based Reinforcement Learning.” International Conference on Machine Learning, pp. 7444-7453. 2019.