Running Julia on Graphcore IPUs

I am a Research Software Developer at University College London and user of the Julia programming language since 2016. I am also curious about trying out Julia on interesing hardware - which led me to implementing it on the Graphcore IPUs. However, I am not a compiler engineer.

You can try running code written in Julia on the IPU for free using a number of sample notebooks on Paperspace Gradient.

Julia

Code demonstration on IPU

You may also like to watch a presentation I gave on implementing Julia on the Graphcore IPU at JuliaCon 2023.

What is Julia?

Julia is a modern, dynamic, general-purpose, compiled programming language. It's interactive ("like Python"), can be used in a REPL or notebooks, like Jupyter (it's the "Ju") or Pluto (this one🎈). Julia has a runtime which includes a just-in-time (JIT) compiler and a garbage collector (GC), for automatic memory management.

Julia is mainly used for numerical computing, diffential equations solvers suite is quite popular.

Main paradigm of Julia is multiple dispatch, what functions do depend on type and number of all arguments.

Why Julia?

Target 1 Target 2

From "My Target Audience" by Matthijs Cox

Explorable & Understandable
Composability thanks to multiple dispatch (ask me more about this at the end!)
User-defined types are as fast and compact as built-ins
Code that is close to the mathematics
No need to switch languages for performance...
...but you can still call C-like shared libraries with simple Foreign Function Interface (FFI) if you want to
MIT licensed: free and open source

My first IPU program in Julia

We developed a package called IPUToolkit.jl to interface the Poplar SDK:


using IPUToolkit.Poplar


let
    # Set up graph and program
    device = Poplar.get_ipu_device()
    target = Poplar.DeviceGetTarget(device)
    graph = Poplar.Graph(target)
    prog = Poplar.ProgramSequence()

    # Create CPU array
    h3 = zeros(Float32, 4, 4)

    # Create IPU tensors
    c1 = Poplar.GraphAddConstant(graph, Float32[1.0, 1.5, 2.0, 2.5])
    v1 = similar(graph, c1, "v1")
    v2 = similar(graph, c1, "v2")
    v3 = similar(graph, h3, "v3")
    v4 = Poplar.GraphAddVariable(graph, Poplar.INT(), UInt64[10], "v4")

    # Tensors tile mapping
    Poplar.GraphSetTileMapping(graph, v1, 0)

    for i in UInt64(0):UInt64(3)
        Poplar.GraphSetTileMapping(graph, v2[i], i)
    end

    Poplar.GraphSetTileMapping(graph, v3, 0)
    Poplar.GraphSetTileMapping(graph, v4, 0)

    Poplar.GraphSetTileMapping(graph, c1, 0)

    # Copy `c1` to `v1` and print `v1`
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(c1, v1))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v1-debug", v1))

    # Copy `v1` to `v2` and print `v2` (should be same as `v1` above)
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(v1, v2))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v2-debug", v2))

    # Prepare copying data between CPU and IPU
    Poplar.GraphCreateHostWrite(graph, "v3-write", v3)
    Poplar.GraphCreateHostRead(graph, "v3-read", v3)

    v1slice = Poplar.TensorSlice(v1, 0, 3)
    v3slice = Poplar.TensorSlice(v3, UInt64[1, 1], UInt64[2, 4])
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(v1slice, v3slice))

    # Read three batches of 10 `Int32`s from the strea `inStream` into `v4` and print values
    inStream = Poplar.GraphAddHostToDeviceFIFO(graph, "v4-input-stream", Poplar.INT(), 10)

    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(inStream, v4))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v4-0", v4))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(inStream, v4))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v4-1", v4))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramCopy(inStream, v4))
    Poplar.ProgramSequenceAdd(prog, Poplar.ProgramPrintTensor("v4-2", v4))

    flags = Poplar.OptionFlags()
    Poplar.OptionFlagsSet(flags, "debug.instrument", "true")

    engine = Poplar.Engine(graph, prog, flags)
    Poplar.EngineLoad(engine, device)

    Poplar.EngineWriteTensor(engine, "v3-write", h3)

    # Create data to stream to `v4`
    inData = Int32.(1:30)

    # Connect data to stream
    Poplar.EngineConnectStream(engine, "v4-input-stream", inData)

    # Run the engine
    Poplar.EngineRun(engine, 0)

    # Write IPU tensor `v3` to CPU array `h3`
    Poplar.EngineReadTensor(engine, "v3-read", h3)

    # Release device
    Poplar.detach_devices()

    # Print value of CPU array `h3`
    print("h3 data: ")
    display(h3')
end


Trying to attach to device 0...
Successfully attached to device 0


v1-debug: [1.0000000 1.5000000 2.0000000 2.5000000]
v2-debug: [1.0000000 1.5000000 2.0000000 2.5000000]
v4-0: [ 1 2 3 4 5 6 7 8 9 10]
v4-1: [11 12 13 14 15 16 17 18 19 20]
v4-2: [21 22 23 24 25 26 27 28 29 30]
h3 data: 4×4 adjoint(::Matrix{Float32}) with eltype Float32:
0.0 0.0 0.0 0.0
0.0 1.0 1.5 2.0
0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0

But we are just writing C++ code in Julia, nothing excitingly new... Can we do more?

What's a compiler?

LysTgpt (1)

(A high-level diagram of a compiler pipeline, with emphasis on the front-end, from "What can we learn from how compilers are designed?")

The only existing implementation of Julia is based on the LLVM compiler, a popular modular compilation framework.

With Julia we can easily inspect each stage of the compilation pipeline.


Meta.@dump 1.0 + 2.0


Expr
head: Symbol call
args: Array{Any}((3,))
1: Symbol +
2: Float64 1.0
3: Float64 2.0


CodeInfo(
1 ─ %1 = Base.add_float(x, y)::Float64
└──      return %1
)                  =>Float64)

@code_typed 1.0 + 2.0


@code_llvm debuginfo=:none 1.0 + 2.0


define double @"julia_+_4759"(double %0, double %1) #0 {
top:
  %2 = fadd double %0, %1
  ret double %2
}


@code_native debuginfo=:none 1.0 + 2.0


 .text
 .file "+"
 .globl "julia_+_4795"                  # -- Begin function julia_+_4795
 .p2align 4, 0x90
 .type "julia_+_4795",@function
"julia_+_4795":                         # @"julia_+_4795"
# %bb.0:                                # %top
 push rbp
 mov rbp, rsp
 vaddsd xmm0, xmm0, xmm1
 pop rbp
 ret
.Lfunc_end0:
 .size "julia_+_4795", .Lfunc_end0-"julia_+_4795"
                                        # -- End function
 .section ".note.GNU-stack","",@progbits

For more details on the Julia compiler watch the talk "Compiling Julia: Making dynamic programs run fast" by Valentin Churavy.

The common factor: LLVM

It turns out also the Poplar compiler, the compiler developed by Graphcore for generating the native code for the IPU, is based on LLVM. When you compile a codelet for the IPU you, the Poplar compiler performs the same pipeline we have seen above.

This means that Julia and the Poplar compiler can actually talk the same language: the LLVM IR.

We added to IPUToolkit.jl the capability to generate code for the IPU with Julia. All in all, this package has the following goals:

interfacing the Poplar SDK for writing an IPU program in Julia
exploring Julia's metaprogramming capabilities for reducing boilerplate code in IPU programs
using Julia code generation capabilities to produce native code for the IPU through the Poplar compiler, using the pipeline outlined in this picture:

LLVM (1)

Writing IPU codelets in Julia

We can use the IPUToolkit.jl package to write IPU codelets in Julia, generating LLVM IR code which is then compiled to native code with the Poplar compiler. The code generation via LLVM is based on the GPUCompiler.jl package, which is a generic framework for generating LLVM IR code for specialised targets, not limited to GPUs despite the historical name.

The code inside a codelet has the same limitations as all the compilation models based on GPUCompiler.jl:

the code has to be statically inferred and compiled, dynamic dispatch is not admitted;
you cannot use functionalities which require the Julia runtime, most notably the garbage collector;
you cannot call into any other external binary library at runtime, for example you cannot call into a BLAS library.

Colossus target and performance

The LLVM IR is mostly target-independent, but not completely. Also, some details, like width of vectorisation registers, can be better tailored for the target if its properties are known correctly. For most of this project I actually generated LLVM IR for the host CPU, which "works", but is not optimal.

I recently managed to link Julia to Graphcore's fork of LLVM, which allowed me to directly generate code for the IPU (the "Colossus" target), however this combination is highly experimental and causes some unexpected errors.

Computing 𝜫

Inspired by Owain Kenway's pi_examples in several different languages.


using IPUToolkit.IPUCompiler


# Disable spinner to show progress of codelet compilation,
# Pluto notebooks have their own progress indicator.
IPUCompiler.PROGRESS_SPINNER[] = false;


# Do not automatically delete LLVM modules of codelets.
IPUCompiler.KEEP_LLVM_FILES[] = true;


# Limit run-time of codelets
ENV["POPLAR_RUNTIME_OPTIONS"] = """{"target.hostSyncTimeout":"60"}""";


let
 device = Poplar.get_ipu_device()
 target = Poplar.DeviceGetTarget(device)
 graph = Poplar.Graph(target)
 
 num_tiles = Int(Poplar.TargetGetNumTiles(target))
 n::UInt32 = typemax(UInt32) ÷ num_tiles
 unroll::UInt32 = 1
 iszero(rem(n, unroll)) || error("n ($(n)) is not an integer multiple of unroll factor ($(unroll))")
 num_steps::UInt32 = num_tiles * n
 slice::Float32 = 1 / num_steps
 
 tile_clock_frequency = Poplar.TargetGetTileClockFrequency(target)
 
 ids = collect(UInt32.(0:(num_tiles - 1)))
 sums = similar(ids, Float32)
 cycles = similar(ids)
 
 # With `@eval` we can interpolate (using `$`) global variables
 # inside the kernel.
 @eval function pi_kernel(i::T) where {T<:Integer}
     sum = 0f0
 for j in (i * $(n)):$(unroll):((i + one(T)) * $(n) - one(T))
 Base.Cartesian.@nexprs $(Int64(unroll)) idx -> begin
 x = (j + Float32(idx - 1) - 0.5f-1) * $(slice)
 sum += 4 / (1 + x ^ 2)
 end
 end
     return sum
 end
 
 @codelet graph function Pi(in::VertexVector{UInt32, In},
                            out::VertexVector{Float32, Out},
                            cycles::VertexVector{UInt32, Out})
     cycles[begin] = @ipuelapsed(out[begin] = pi_kernel(in[begin]))
 end
 
 # Type and shape of tensors automatically inferred from input arrays
 ids_ipu = Poplar.GraphAddConstant(graph, ids)
 sums_ipu = similar(graph, sums, Float32, "sums");
 cycles_ipu = similar(graph, cycles, UInt32, "cycles");
 
 prog = Poplar.ProgramSequence()
 
 # Automatically add the codelet defined above to the program
 # and spread it across all the tiles
 add_vertex(graph, prog, 0:(num_tiles - 1), Pi, ids_ipu, sums_ipu, cycles_ipu)
 
 # Simplified API for `GraphCreateHostRead`, we can use fewer arguments
 Poplar.GraphCreateHostRead(graph, "sums-read", sums_ipu)
 Poplar.GraphCreateHostRead(graph, "cycles-read", cycles_ipu)
 
 engine = Poplar.Engine(graph, prog)
 Poplar.EngineLoadAndRun(engine, device)
 
 # Simplified API also for `EngineReadTensor`
 Poplar.EngineReadTensor(engine, "sums-read", sums)
 Poplar.EngineReadTensor(engine, "cycles-read", cycles)
 
 Poplar.detach_devices()
 
 pi = sum(sums) * slice
 time = round(maximum(cycles) / tile_clock_frequency; sigdigits=4)
 
 print("""
          Calculating PI using:
            $(num_steps) slices
            $(num_tiles) IPU tiles
            loop unroll factor $(Int(unroll))
          Obtained value of PI: $(pi)
          Time taken: $(time) seconds ($(maximum(cycles)) cycles at $(round(tile_clock_frequency / 1e9; sigdigits=3)) GHz)
          """)
end;


Trying to attach to device 0...
Successfully attached to device 0


Calculating PI using:
4294966272 slices
1472 IPU tiles
loop unroll factor 1
Obtained value of PI: 3.1499734
Time taken: 0.123 seconds (227586882 cycles at 1.85 GHz)

Comparison with C++ program

We can write an equivalent C++ program to compare performance, to check how Julia code generation is faring. This is the codelet:


#include <poplar/Vertex.hpp>

using namespace poplar;

class VertexPi : public Vertex {
public:
    Input<unsigned> id;
    Input<unsigned> n;
    Input<float> slice;
    Output<Vector<float>> out;
    Output<Vector<unsigned>> cycles;

    bool compute() {
        float sum = 0;
        unsigned start = __builtin_ipu_get_scount_l();
        for (unsigned j=id * n; j < (id + 1) * n; j++) {
            float x = (j - 0.5f) * slice;
            sum += 4.0f / (1.0f + x * x);
        }
        unsigned end = __builtin_ipu_get_scount_l();
        out[0] = sum;
        cycles[0] = end - start;
        return true;
    }
};


run(`$(cpp_exe_path)`);


Using HW device ID: 0
Calculating PI using:
4294966272 slices
1472 IPU tiles
Obtained value of PI: 0.146298
Time taken: 0.141946 seconds (262599924 cycles at 1.85 GHz)

Main performance difference between the C++ and the Julia codelets in this case is due to loop unrolling. Some experimentations showed that when both code have loops similarly unrolled then performance is perfectly comparable. This showed that Julia can be a valid front-end for writing code for the IPU.

Benchmarking within codelets

IPUToolkit.jl provides some macros for quickly benchmarking parts of a codelet: @ipucycles, @ipushowcycles, @ipuelapsed (the latter was already used above).


let
 device = Poplar.get_ipu_device()
    target = Poplar.DeviceGetTarget(device)
    graph = Poplar.Graph(target)
 
    @codelet graph function Benchmark(input::VertexVector{Float32, In},
   output::VertexVector{Float32, Out})
        for idx in eachindex(input, output)
            x = input[idx]
            @ipushow x
            x = @ipushowcycles sin(x)
            x = @ipushowcycles cos(x)
            x = @ipushowcycles exp(x)
            output[idx] = x
        end
    end
 
    in_ipu = Poplar.GraphAddConstant(graph, randn(Float32, 5))
    out_ipu = similar(graph, in_ipu);
 
    prog = Poplar.ProgramSequence()
 
    add_vertex(graph, prog, Benchmark, in_ipu, out_ipu)
 
    engine = Poplar.Engine(graph, prog)
    Poplar.EngineLoadAndRun(engine, device)
    Poplar.detach_devices()
end


Trying to attach to device 0...
Successfully attached to device 0


T[0.5]: x = 0.433483
T[0.5]: sin(x):
T[0.5]: 14418 cycles
T[0.5]: cos(x):
T[0.5]: 13320 cycles
T[0.5]: exp(x):
T[0.5]: 18 cycles
T[0.5]: x = -1.012771
T[0.5]: sin(x):
T[0.5]: 14448 cycles
T[0.5]: cos(x):
T[0.5]: 15834 cycles
T[0.5]: exp(x):
T[0.5]: 18 cycles
T[0.5]: x = 0.436158
T[0.5]: sin(x):
T[0.5]: 14430 cycles
T[0.5]: cos(x):
T[0.5]: 13302 cycles
T[0.5]: exp(x):
T[0.5]: 18 cycles
T[0.5]: x = 1.835203
T[0.5]: sin(x):
T[0.5]: 14562 cycles
T[0.5]: cos(x):
T[0.5]: 15798 cycles
T[0.5]: exp(x):
T[0.5]: 18 cycles
T[0.5]: x = -0.725937
T[0.5]: sin(x):
T[0.5]: 14592 cycles
T[0.5]: cos(x):
T[0.5]: 13308 cycles
T[0.5]: exp(x):
T[0.5]: 18 cycles

Note: This isn't a replacement for profiling, which is still an invaluable tool (but JIT complicats stacktraces), however these macros can be useful for quick feedback.

Cycle-count-based benchmarking is not reliable for blocks taking longer than typemax(UInt32) = 4294967295 cycles, about 2-3 seconds depending on your IPU model. You need to have a feeling whether the block you want to benchmark would overflow the counter.

Using external packages: StaticArrays.jl

We can also use third-party packages inside codelets, as long as the requirements mentioned above are met: no memory allocations, fully inferrable code. The StaticArrays.jl allows you to create arrays on the stack and do basic linear algebra operations with them. Code involving static arrays is also usally easy to infer for the compiler.

StaticArrays.jl isn't more efficient than using specialised Popops linear algebra routines, but nonetheless is a good example of usage of external packages inside IPU codelets written in Julia.


using StaticArrays


let
 device = Poplar.get_ipu_device()
 target = Poplar.DeviceGetTarget(device)
 graph = Poplar.Graph(target)
 
 N = 16
    mat1 = randn(Float32, N)
    mat2 = randn(Float32, N)
 
    mul = PoplarVector{Float32}(undef, N)
    inverse = PoplarVector{Float32}(undef, N)
 
    @ipuprogram device begin
        function MatMul(in1::VertexVector{Float32, In},
 in2::VertexVector{Float32, In},
 mul::VertexVector{Float32, Out})
            m1 = @inbounds SMatrix{4,4,Float32,16}(in1)
            m2 = @inbounds SMatrix{4,4,Float32,16}(in2)
            mul .= (m1 * m2)[:]
        end
        function Inverse(input::VertexVector{Float32, In},
 inverse::VertexVector{Float32, Out})
            m = @inbounds SMatrix{4,4,Float32,16}(input)
            inverse .= inv(m)[:]
        end
 
        MatMul(mat1, mat2, mul)
        Inverse(mul, inverse)
 
        jl_mul = mul
        jl_inv = inverse
    end
    Poplar.detach_devices()
 
 jl_mul = reshape(jl_mul, 4, 4)
 @show reshape(mat1, 4, 4) * reshape(mat2, 4, 4) ≈ jl_mul
 @show reshape(jl_inv, 4, 4) ≈ inv(jl_mul)
end;


Trying to attach to device 0...
Successfully attached to device 0


reshape(mat1, 4, 4) * reshape(mat2, 4, 4) ≈ jl_mul = true
reshape(jl_inv, 4, 4) ≈ inv(jl_mul) = true

Stochastic rounding

Real numbers constitue a continuous set \(\mathbb{R}\), but finite precision numbers used in computers are a part of a discrete set \(F\subset\mathbb{R}\). When computers do operations involving floating point numbers in \(F\), the true result \(x\in\mathbb{R}\) will be approximated by a number \(\hat x \in F\), which is typically chosen deterministically to be the nearest number in \(F\): this is called "nearest rounding".

Stochastic rounding is an alternative rounding mode to classic deterministic rounding, which randomly rounds a number \(x\in\mathbb{R}\) to either of the two nearest floating point numbers of the result \([x]\) (previous number in \(F\)) or \([x]\) (following number in \(F\)) with the following rule:

2023-09-07 09 57 30 Common choices are \(P(x) = 1/2\) or, more interestingly,

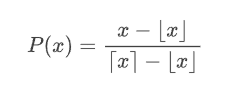2023-09-07 09 57 34 In the following we'll always talk about the latter probability function \(P(x)\).

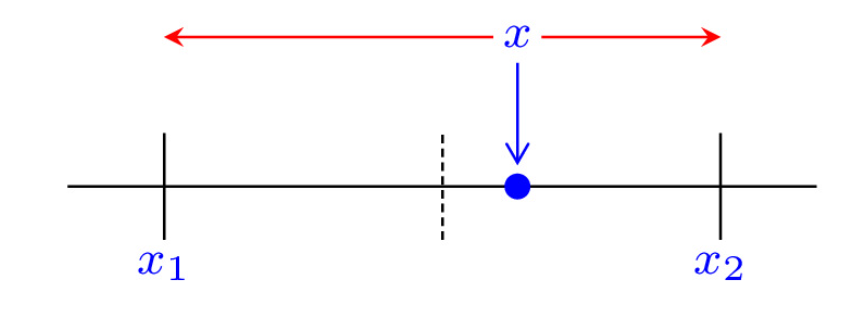2023-09-07 10 07 29 (source: "What Is Stochastic Rounding?" by Nick Higham)

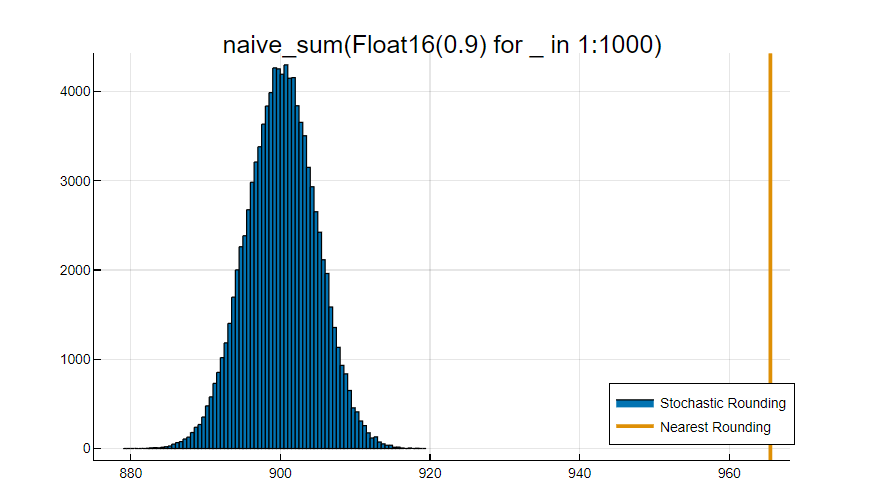
Stochastic rounding is useful because the average result of operations matches the expected mathematical result. In a statistical sense, it retains some of the information that is discarded by a deterministic rounding scheme, smoothing out numerical rounding errors due to limited precisions. This is particularly important when using low-precision floating point numbers like Float16. For contrast, deterministic rounding modes like nearest rounding introduce a bias, which is more severe as the precision of the numbers is lower.

The IPU is one of the very few processors available with hardware support for stochastic rounding.

Let's do an exercise on the CPU with classical nearest rounding. We define a function to do the naive sequential sum of a vector of numbers, because the sum function in Julia uses pairwise summation, which would have better accuracy.

naive_sum (generic function with 1 method)


naive_sum(v) = foldl(+, v)


x_sr = fill(Float16(0.9), 1000);

Float16(965.5)


naive_sum(x_sr)

false


naive_sum(x_sr) ≈ x_sr[1] * length(x_sr)

Now let's write an IPU program which computes the sum of x_sr multiple times with stochastic rounding:


sums_sr = let
    device = Poplar.get_ipu_device()
    target = Poplar.DeviceGetTarget(device)
    graph = Poplar.Graph(target)
    prog = Poplar.ProgramSequence()
    Poplar.PoplarSetStochasticRounding(graph, prog, true, "")
 
    @codelet graph function stochastic_rounding(x::VertexVector{Float16, In}, sums::VertexVector{Float16, Out})
        for idx in eachindex(sums)
            sums[idx] = naive_sum(x)
        end
    end
 
 sums_sr = Vector{Float16}(undef, 100_000)
    x_ipu =  Poplar.GraphAddConstant(graph, x_sr)
    sums_ipu = similar(graph, sums_sr)
    add_vertex(graph, prog, stochastic_rounding, x_ipu, sums_ipu)
 
    # Prepare tensors read
    Poplar.GraphCreateHostRead(graph, "sums-read", sums_ipu)
 
    # Run the program
    engine = Poplar.Engine(graph, prog)
    Poplar.EngineLoadAndRun(engine, device)
 
    # Read the output tensors back to the CPU
    Poplar.EngineReadTensor(engine, "sums-read", sums_sr)
 
    Poplar.detach_devices()
 
 sums_sr
end;


Trying to attach to device 0...
Successfully attached to device 0


using Plots: plot, plot!, contour, surface, heatmap, histogram, vline!, plotlyjs


import PlotlyJS


plotlyjs();


using Statistics

(879.0, 919.0)


extrema(sums_sr)

899.90252


mean(Float64.(sums_sr))

4.683982498528412


std(Float64.(sums_sr))

Float16(900.0)


median(sums_sr)

true


all(isapprox(sum(Float64.(x_sr))), sums_sr)

Solving differential equations on the IPU

If we want to use external packages on the IPU, we can look for similar solutions for the GPU. If they have been made generic enough to work with different backends chances are good that they can be used on the IPU as well.

An example is DiffEqGPU.jl, a suite of differential equations solvers part of the SciML ecosystem that can be run on different kinds of GPUs (Nvidia, AMD, Intel, Metal), but it provides basic functionalities that we can reuse on the IPU as well.


using DiffEqGPU, OrdinaryDiffEq


N_lotka_volterra = 20_000;


begin
    T_lotka_volterra = Float16
    α_lotka_volterra_range = range(T_lotka_volterra(0.1); step=T_lotka_volterra(0.1), length=64)
    β_lotka_volterra_range = range(T_lotka_volterra(0.1); step=T_lotka_volterra(0.1), length=23)
end;


# Create a range of different input parameters
lotka_volterra_parameters = let
    α = repeat(α_lotka_volterra_range; inner=23)
    β = repeat(β_lotka_volterra_range; outer=64)
    γ = repeat([T_lotka_volterra(3)], length(β))
    δ = repeat([T_lotka_volterra(1)], length(β))
    zip(α, β, γ, δ) |> Iterators.flatten |> collect
end;


function lotka_volterra(u, p, t)
    α, β, γ, δ = p
    🐰, 🦊 = u
    d🐰 = α * 🐰 - β * 🐰 * 🦊
    d🦊 = -γ * 🦊 + δ * 🐰 * 🦊
    return SVector{2}(d🐰, d🦊)
end;


function lotka_volterra_cpu(p::Vector,
 n::Integer,
 timestep::Real,
 FT::DataType=Float64)
 u1 = Vector{FT}(undef, n)
 u2 = Vector{FT}(undef, n)
 u0 = @SVector [FT(1); FT(1)]
    svp = @inbounds SVector{4, FT}(p)
    integ = DiffEqGPU.init(GPUTsit5(), lotka_volterra, false, u0, FT(0), FT(timestep), svp, nothing, CallbackSet(nothing), true, false)
 
 for idx in eachindex(u1, u2)
        DiffEqGPU.step!(integ, integ.t + integ.dt, integ.u)
        u1[idx] = integ.u[1]
        u2[idx] = integ.u[2]
    end
 
 return u1, u2
end;


u1_16, u2_16, u1_16_sr, u2_16_sr = let
 device = Poplar.get_ipu_device()
 target = Poplar.DeviceGetTarget(device)
 graph = Poplar.Graph(target)
 
 tile_clock_frequency = Poplar.TargetGetTileClockFrequency(target)
 num_tiles = Int(Poplar.TargetGetNumTiles(target))
 tiles = 0:(num_tiles - 1)
 
 @codelet graph function solve_lv(u1::VertexVector{Float16, Out},
                               u2::VertexVector{Float16, Out},
                                  p::VertexVector{Float16, In},
 cycles::VertexVector{UInt32, Out})
     u0 = @SVector [Float16(1); Float16(1)]
     svp = @inbounds SVector{4, Float16}(p)
     integ = DiffEqGPU.init(GPUTsit5(), lotka_volterra, false, u0, Float16(0), Float16(0.001), svp, nothing, CallbackSet(nothing), true, false)
     cycles[begin] = @ipuelapsed for idx in eachindex(u1, u2)
         DiffEqGPU.step!(integ, integ.t + integ.dt, integ.u)
         u1[idx] = integ.u[1]
         u2[idx] = integ.u[2]
     end
 end
 
 FT = T_lotka_volterra
 len = N_lotka_volterra * (length(lotka_volterra_parameters) ÷ 4)
 u1_16 = Vector{FT}(undef, len)
 u2_16 = Vector{FT}(undef, len)
 u1_16_sr = Vector{FT}(undef, len)
 u2_16_sr = Vector{FT}(undef, len)
 cycles = Vector{UInt32}(undef, num_tiles)
 cycles_sr = Vector{UInt32}(undef, num_tiles)
 
 p_ipu =  Poplar.GraphAddConstant(graph, lotka_volterra_parameters)
 
 # Convenient function for defining the name of a read operation
 _read(name::String, sr::Bool) = "$(name)-$(sr ? "sr-" : "")read"
 
 for sr in (true, false)
 prog = Poplar.ProgramSequence()
 Poplar.PoplarSetStochasticRounding(graph, prog, sr, "")
 
 u1_ipu = similar(graph, sr ? u1_16_sr : u1_16)
 u2_ipu = similar(graph, sr ? u2_16_sr : u2_16)
 cycles_ipu = similar(graph, sr ? cycles_sr : cycles)
 
 # Run the codelet defined above on all tiles,
 # with tensors evenly spread across all cores.
 add_vertex(graph, prog, tiles, solve_lv, u1_ipu, u2_ipu, p_ipu, cycles_ipu)
 
 # Prepare tensors read
 Poplar.GraphCreateHostRead(graph, _read("u1", sr), u1_ipu)
 Poplar.GraphCreateHostRead(graph, _read("u2", sr), u2_ipu)
 Poplar.GraphCreateHostRead(graph, _read("cycles", sr), cycles_ipu)
 
 # Run the program
 engine = Poplar.Engine(graph, prog)
 Poplar.EngineLoadAndRun(engine, device)
 
 # Read the output tensors back to the CPU
 Poplar.EngineReadTensor(engine, _read("u1", sr), sr ? u1_16_sr : u1_16)
 Poplar.EngineReadTensor(engine, _read("u2", sr), sr ? u2_16_sr : u2_16)
 Poplar.EngineReadTensor(engine, _read("cycles", sr), sr ? cycles_sr : cycles)
 end
 
 Poplar.detach_devices()
 
 time = round(maximum(cycles) / tile_clock_frequency; sigdigits=3)
 time_sr = round(maximum(cycles_sr) / tile_clock_frequency; sigdigits=3)
 
 @info "Solving $(length(lotka_volterra_parameters) ÷ 4) ODEs on $(num_tiles) tiles took $(time) seconds with NR, and $(time_sr) with SR."
 
 u1_16, u2_16, u1_16_sr, u2_16_sr
end;


Trying to attach to device 0...
Successfully attached to device 0
Solving 1472 ODEs on 1472 tiles took 0.0145 seconds with NR, and 0.0145 with SR.

2023-09-18 09 53 44

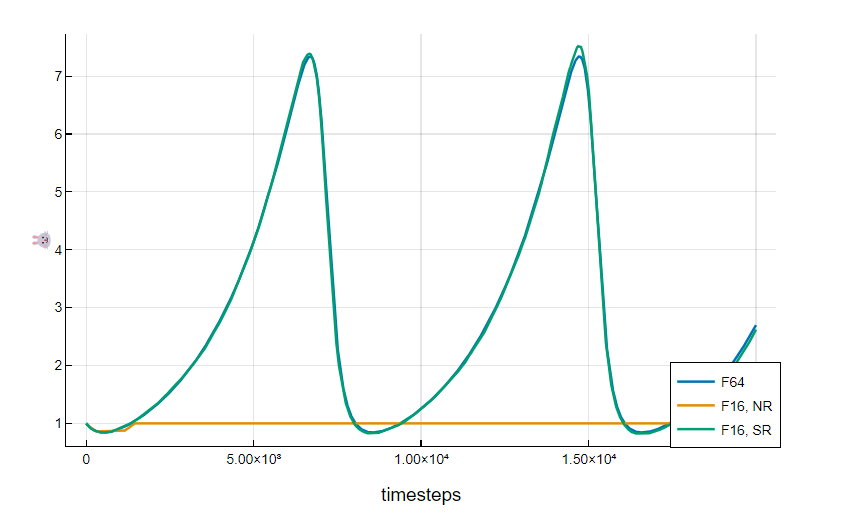Automatic differentiation

In mathematics, contrary to integration, computing the derivative of an expression is a mechanical process. Wouldn't it be nice to automatically compute the exact derivative of mathematical functions in your code?

Automatic differentiation (autodiff in short) is a set of techniques to automatically compute the derivative of a function in a computer program.

Enzyme is a source code transformation autodiff engine operating at the LLVM level: it analysis the LLVM IR of the source code and takes the derivative of all the instructions, based on the built-in differentiation rules. The fact that it works at the LLVM level means that it's mostly front-end-language-agnostic and can be used to take derivative of source code combining multiple languages or using parallelisation frameworks ("Scalable automatic differentiation of multiple parallel paradigms through compiler augmentation" won Best Student Paper award at SuperComputing 2022). Also, Enzyme generates code at compile-time, it doesn't run itself on the target system: it's the perfect candidate for use in an IPU program!


using Enzyme


Enzyme.Compiler.enzyme_code_llvm(stdout, sin, Active, Tuple{Active{Float64}})


; Function Attrs: alwaysinline nofree nosync readnone
define [1 x [1 x double]] @diffejulia_sin_10561mustwrap_inner_1wrap(double %0, double %1) #2 {
entry:
%2 = call fast double @llvm.cos.f64(double %0)
%3 = fmul fast double %2, %1
%.unpack1 = insertvalue [1 x double] zeroinitializer, double %3, 0
%4 = insertvalue [1 x [1 x double]] zeroinitializer, [1 x double] %.unpack1, 0
ret [1 x [1 x double]] %4
}

Rosenbrock function

Evereyone's favourite example function for optimisation problems.

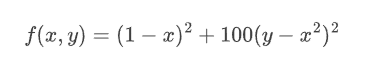
2023-09-07 12 41 33

rosenbrock (generic function with 2 methods)


rosenbrock(x, y=4) = (1 - x) ^ 2 + 100 * (y - x ^ 2) ^ 2

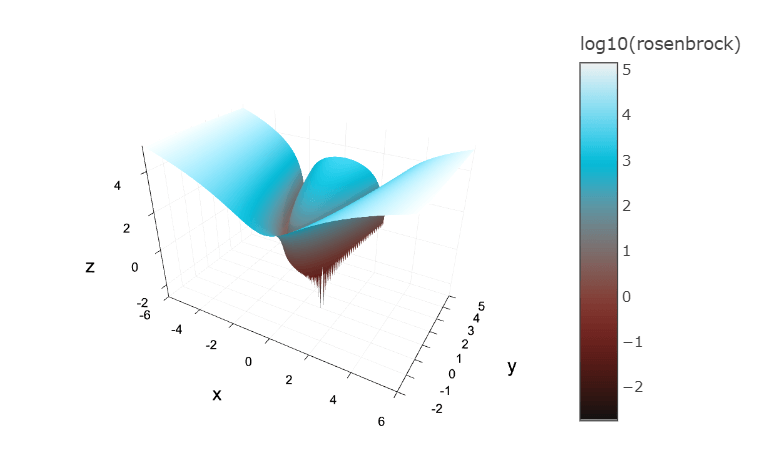
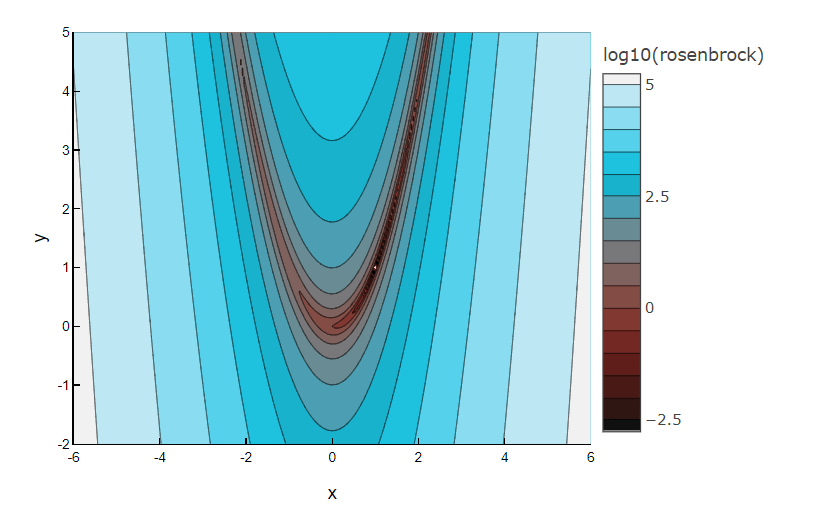2023-09-07 13 00 28 2023-09-07 13 00 38 Finding the valley is trivial, but converging to the global minimum is hard.

The Rosenbrock function is a polynomial function, easy to compute its gradient:

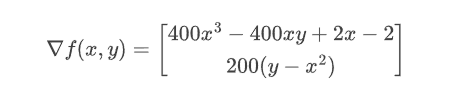2023-09-07 13 04 57 We can ask Enzyme to compute the partial derivative on the second argument:


Enzyme.Compiler.enzyme_code_llvm(stdout, rosenbrock, Active, Tuple{Const{Float64}, Active{Float64}})


;  @ /home/cceamgi/repo/rsdg-meetings/2023-07-20-julia-ipu/julia-ipu.jl#==#c30b8552-03f4-4f79-b4c0-7179ead69192 within `diffejulia_rosenbrock_11601_inner_1wrap`
; Function Attrs: alwaysinline nofree
define [1 x { double }] @diffejulia_rosenbrock_11601_inner_1wrap(double %0, double %1, double %2) #1 {
entry:
  %thread_ptr = call i8* asm "movq %fs:0, $0", "=r"() #6
  %tls_ppgcstack = getelementptr i8, i8* %thread_ptr, i64 -8
  %3 = bitcast i8* %tls_ppgcstack to {}****
  %tls_pgcstack = load {}***, {}**** %3, align 8
  %ptls_field.i2.i = getelementptr inbounds {}**, {}*** %tls_pgcstack, i64 2
  %4 = bitcast {}*** %ptls_field.i2.i to i64***
  %ptls_load.i34.i = load i64**, i64*** %4, align 8
  %5 = getelementptr inbounds i64*, i64** %ptls_load.i34.i, i64 2
  %safepoint.i.i = load i64*, i64** %5, align 8
  fence syncscope("singlethread") seq_cst
; ┌ @ /home/cceamgi/repo/rsdg-meetings/2023-07-20-julia-ipu/julia-ipu.jl#==#c30b8552-03f4-4f79-b4c0-7179ead69192 within `rosenbrock` @ /home/cceamgi/repo/rsdg-meetings/2023-07-20-julia-ipu/julia-ipu.jl#==#c30b8552-03f4-4f79-b4c0-7179ead69192:1
   %6 = load volatile i64, i64* %safepoint.i.i, align 8
   fence syncscope("singlethread") seq_cst
; │┌ @ intfuncs.jl:332 within `literal_pow`
; ││┌ @ float.jl:411 within `*`
     %7 = fmul double %0, %0
; │└└
; │┌ @ float.jl:410 within `-`
    %8 = fsub double %1, %7
; │└
; │┌ @ intfuncs.jl:332 within `literal_pow`
; ││┌ @ float.jl:411 within `*`
     %9 = fmul fast double %2, 2.000000e+02
     %10 = fmul fast double %9, %8
     fence syncscope("singlethread") seq_cst
     %.unpack1 = insertvalue { double } zeroinitializer, double %10, 0
     %11 = insertvalue [1 x { double }] zeroinitializer, { double } %.unpack1, 0
     ret [1 x { double }] %11
; └└└
}

Minimising a function with Enzyme

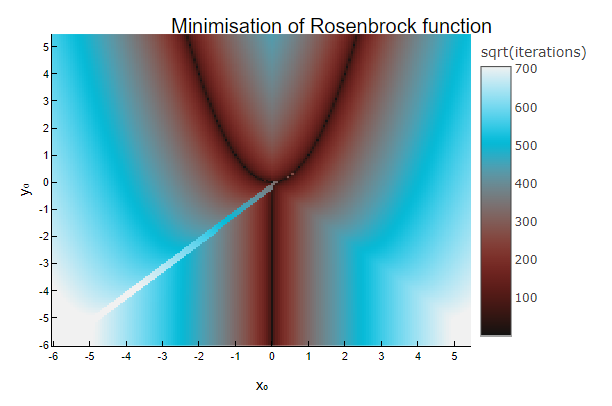
We can run an IPU program to find the minima of the Rosenbrock function on a large grid of different starting points, and plot the number of iterations taken before stopping, when the terminating criteria are met. In particular, we will use the Adam, an optimisation method which requires the gradient of the function to optimise as input, and we will use Enzyme to automatically compute it on the host system at compile time.


rosenbrock(x, y) = (1 - x) ^ 2 + 100 * (y - x ^ 2) ^ 2;


∂(f, x, y) = first(autodiff_deferred(Reverse, f, Active(x), Active(y)));


rosenbrock′(x, y) = ∂(rosenbrock, x, y);


function adam(∂f, x₀::T, y₀::T) where {T}
    x, y = x₀, y₀
    # Some constants
    α = T(0.001) # learning rate
    β₁ = T(0.9)
    β₂ = T(0.999)
    ϵ = T(1e-8)
    # Momenta
    m = zero(T), zero(T)
    v = zero(T), zero(T)
    # Stopping criteria
    Δ = 10 * eps(T)
    δ_x, δ_y = one(T), one(T)
    max_t = Int32(500_000)
    t = one(max_t)
    while abs(δ_x) > Δ < abs(δ_y) && t ≤ max_t
      g = ∂f(x, y)
      m = β₁ .* m .+ (1 - β₂) .* g
      v = β₂ .* v .+ (1 - β₂) .* g .^ 2
      m̂ = m ./ (1 - β₁ ^ t)
      v̂ = v ./ (1 - β₂ ^ t)
      δ_x, δ_y = α .* m̂ ./ (.√(v̂) .+ ϵ)
      x -= δ_x
      y -= δ_y
      t += one(t)
    end
 # Subtract one because at the end of the last iteration we
 # added 1 to the counter but didn't run the following iteration.
    return t - one(t)
end;


begin
 make_grid(x::T, y::T) where {T<:AbstractVector} =
     repeat(x; inner=length(y)), repeat(y; outer=length(x))
 
 # High resolution range
 x_range = y_range = collect(Float32.(range(-6; step=2^-4, length=23 * 8)))
 
 # # Low resolution range
 # x_range = collect(Float32.(range(-6; step=2^-2, length=23 * 2)))
 # y_range = collect(Float32.(range(-8; step=2^-2, length=64)))
end;


m = let
 # Inputs to the codelet
 x₀, y₀ = make_grid(x_range, y_range)
 # Output of the codelet
 num_iterations = similar(x₀, Int32)
 
 device = Poplar.get_ipu_device()
 target = Poplar.DeviceGetTarget(device)
 graph = Poplar.Graph(target)
 
 num_tiles = Int(Poplar.TargetGetNumTiles(target))
 
 @codelet graph function RosenAdam(x::VertexVector{Float32, In},
                                   y::VertexVector{Float32, In},
                                   num_iterations::VertexVector{Int32, Out})
     for idx in eachindex(num_iterations)
         num_iterations[idx] = adam(rosenbrock′, x[idx], y[idx])
     end
 end
 
 x₀_ipu = Poplar.GraphAddConstant(graph, x₀)
 y₀_ipu = Poplar.GraphAddConstant(graph, y₀)
 num_iterations_ipu = similar(graph, num_iterations, Int32);
 
 prog = Poplar.ProgramSequence()
 
 add_vertex(graph, prog, 0:(num_tiles - 1), RosenAdam, x₀_ipu, y₀_ipu, num_iterations_ipu)
 
 Poplar.GraphCreateHostRead(graph, "iterations-read", num_iterations_ipu)
 
 engine = Poplar.Engine(graph, prog)
 elapsed = @elapsed Poplar.EngineLoadAndRun(engine, device)
 Poplar.EngineReadTensor(engine, "iterations-read", num_iterations)
 
 Poplar.detach_devices()
 
 m = reshape(sqrt.(Int.(num_iterations)), length(y_range), length(x_range))
 
 @info "Loading and running the program on $(length(x₀)) points took $(round(elapsed; sigdigits=4)) seconds"
 
 m
end;


Trying to attach to device 0...
Successfully attached to device 0
Loading and running the program on 33856 points took 30.06 seconds

2023-09-07 13 16 16


; ModuleID = 'start'
source_filename = "start"
target datalayout = "e-m:e-p270:32:32-p271:32:32-p272:64:64-i64:64-f80:128-n8:16:32:64-S128"
target triple = "x86_64-linux-gnu"

define void @_Z13_333___Pi_235() local_unnamed_addr #0 !dbg !35 {
top:
  %0 = call i64 @get_vec_ptr_Pi(i32 0), !dbg !39
  %1 = call i32 @get_vec_size_Pi(i32 0), !dbg !39
  %2 = call i64 @get_vec_ptr_Pi(i32 1), !dbg !39
  %3 = call i32 @get_vec_size_Pi(i32 1), !dbg !39
  %4 = call i64 @get_vec_ptr_Pi(i32 2), !dbg !39
  %5 = call i32 @get_vec_size_Pi(i32 2), !dbg !39
  %6 = call i32 @llvm.colossus.get.scount.l(), !dbg !40
  %coercion = inttoptr i64 %0 to i32*, !dbg !49
  %pointerref = load i32, i32* %coercion, align 1, !dbg !49, !tbaa !61, !alias.scope !65, !noalias !68
  %7 = call fastcc float @julia_pi_kernel_5874(i32 zeroext %pointerref), !dbg !60
  %coercion1 = inttoptr i64 %2 to float*, !dbg !73
  store float %7, float* %coercion1, align 1, !dbg !73, !tbaa !61, !alias.scope !65, !noalias !68
  %8 = call i32 @llvm.colossus.get.scount.l(), !dbg !81
  %9 = sub i32 %8, %6, !dbg !83
  %coercion2 = inttoptr i64 %4 to i32*, !dbg !87
  store i32 %9, i32* %coercion2, align 1, !dbg !87, !tbaa !61, !alias.scope !65, !noalias !68
  ret void, !dbg !91
}

declare i64 @get_vec_ptr_Pi(i32) local_unnamed_addr

declare i32 @get_vec_size_Pi(i32) local_unnamed_addr

declare i32 @llvm.colossus.get.scount.l() local_unnamed_addr

define internal fastcc float @julia_pi_kernel_5874(i32 zeroext %0) unnamed_addr #0 !dbg !92 {
top:
  %1 = mul i32 %0, 2917776, !dbg !93
  %.not16 = icmp ult i32 %1, -2917775, !dbg !96
  %value_phi.v = select i1 %.not16, i32 2917775, i32 -1, !dbg !101
  %value_phi = add i32 %1, %value_phi.v, !dbg !101
  %.not = icmp ugt i32 %1, %value_phi, !dbg !111
  br i1 %.not, label %L78, label %L56, !dbg !95

L56:                                              ; preds = %L56, %top
  %value_phi4 = phi i32 [ %9, %L56 ], [ %1, %top ]
  %value_phi6 = phi float [ %8, %L56 ], [ 0.000000e+00, %top ]
  %2 = uitofp i32 %value_phi4 to float, !dbg !118
  %3 = fadd float %2, 0xBFA99999A0000000, !dbg !132
  %4 = fmul float %3, 0x3DF0000040000000, !dbg !134
  %5 = fmul float %4, %4, !dbg !136
  %6 = fadd float %5, 1.000000e+00, !dbg !141
  %7 = fdiv float 4.000000e+00, %6, !dbg !144
  %8 = fadd float %value_phi6, %7, !dbg !148
  %.not15 = icmp eq i32 %value_phi4, %value_phi, !dbg !149
  %9 = add i32 %value_phi4, 1, !dbg !151
  br i1 %.not15, label %L78, label %L56, !dbg !152

L78:                                              ; preds = %L56, %top
  %value_phi10 = phi float [ 0.000000e+00, %top ], [ %8, %L56 ]
  ret float %value_phi10, !dbg !153
}

attributes #0 = { "probe-stack"="inline-asm" }

!llvm.module.flags = !{!0, !1}
!llvm.dbg.cu = !{!2, !4, !5, !6, !7, !8, !9, !10, !11, !12, !13, !14, !15, !16, !17, !18, !19, !20, !21, !22, !23, !24, !25, !26, !27, !28, !29, !30, !31, !32, !33}
!julia.kernel = !{!34}

!0 = !{i32 2, !"Dwarf Version", i32 4}
!1 = !{i32 2, !"Debug Info Version", i32 3}
!2 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!3 = !DIFile(filename: "julia", directory: ".")
!4 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!5 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!6 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!7 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!8 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!9 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!10 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!11 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!12 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!13 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!14 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!15 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!16 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!17 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!18 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!19 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!20 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!21 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!22 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!23 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!24 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!25 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!26 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!27 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!28 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!29 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!30 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!31 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!32 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!33 = distinct !DICompileUnit(language: DW_LANG_Julia, file: !3, producer: "julia", isOptimized: true, runtimeVersion: 0, emissionKind: LineTablesOnly, nameTableKind: None)
!34 = !{void ()* @_Z13_333___Pi_235}
!35 = distinct !DISubprogram(name: "#333###Pi#235", linkageName: "julia_#333###Pi#235_5871", scope: null, file: !36, line: 68, type: !37, scopeLine: 68, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!36 = !DIFile(filename: "/home/cceamgi/.julia/packages/IPUToolkit/1u83e/src/compiler/codelet.jl#@#==#892eee7a-73be-4479-8d00-6e1ee8bdd97b", directory: ".")
!37 = !DISubroutineType(types: !38)
!38 = !{}
!39 = !DILocation(line: 69, scope: !35)
!40 = !DILocation(line: 45, scope: !41, inlinedAt: !43)
!41 = distinct !DISubprogram(name: "get_scount_l;", linkageName: "get_scount_l", scope: !42, file: !42, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!42 = !DIFile(filename: "/home/cceamgi/.julia/packages/IPUToolkit/1u83e/src/compiler/runtime.jl", directory: ".")
!43 = !DILocation(line: 100, scope: !44, inlinedAt: !46)
!44 = distinct !DISubprogram(name: "macro expansion;", linkageName: "macro expansion", scope: !45, file: !45, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!45 = !DIFile(filename: "/home/cceamgi/.julia/packages/IPUToolkit/1u83e/src/compiler/timing.jl#@#==#892eee7a-73be-4479-8d00-6e1ee8bdd97b", directory: ".")
!46 = !DILocation(line: 35, scope: !47, inlinedAt: !39)
!47 = distinct !DISubprogram(name: "Pi;", linkageName: "Pi", scope: !48, file: !48, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!48 = !DIFile(filename: "/home/cceamgi/repo/rsdg-meetings/2023-07-20-julia-ipu/julia-ipu.jl#==#892eee7a-73be-4479-8d00-6e1ee8bdd97b", directory: ".")
!49 = !DILocation(line: 119, scope: !50, inlinedAt: !52)
!50 = distinct !DISubprogram(name: "unsafe_load;", linkageName: "unsafe_load", scope: !51, file: !51, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!51 = !DIFile(filename: "pointer.jl", directory: ".")
!52 = !DILocation(line: 46, scope: !53, inlinedAt: !55)
!53 = distinct !DISubprogram(name: "getindex;", linkageName: "getindex", scope: !54, file: !54, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!54 = !DIFile(filename: "/home/cceamgi/.julia/packages/IPUToolkit/1u83e/src/compiler/vertices.jl", directory: ".")
!55 = !DILocation(line: 1336, scope: !56, inlinedAt: !58)
!56 = distinct !DISubprogram(name: "_getindex;", linkageName: "_getindex", scope: !57, file: !57, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!57 = !DIFile(filename: "abstractarray.jl", directory: ".")
!58 = !DILocation(line: 1286, scope: !59, inlinedAt: !60)
!59 = distinct !DISubprogram(name: "getindex;", linkageName: "getindex", scope: !57, file: !57, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!60 = !DILocation(line: 101, scope: !44, inlinedAt: !46)
!61 = !{!62, !62, i64 0}
!62 = !{!"jtbaa_data", !63, i64 0}
!63 = !{!"jtbaa", !64, i64 0}
!64 = !{!"jtbaa"}
!65 = !{!66}
!66 = !{!"jnoalias_data", !67}
!67 = !{!"jnoalias"}
!68 = !{!69, !70, !71, !72}
!69 = !{!"jnoalias_gcframe", !67}
!70 = !{!"jnoalias_stack", !67}
!71 = !{!"jnoalias_typemd", !67}
!72 = !{!"jnoalias_const", !67}
!73 = !DILocation(line: 146, scope: !74, inlinedAt: !75)
!74 = distinct !DISubprogram(name: "unsafe_store!;", linkageName: "unsafe_store!", scope: !51, file: !51, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!75 = !DILocation(line: 42, scope: !76, inlinedAt: !77)
!76 = distinct !DISubprogram(name: "setindex!;", linkageName: "setindex!", scope: !54, file: !54, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!77 = !DILocation(line: 1419, scope: !78, inlinedAt: !79)
!78 = distinct !DISubprogram(name: "_setindex!;", linkageName: "_setindex!", scope: !57, file: !57, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!79 = !DILocation(line: 1389, scope: !80, inlinedAt: !60)
!80 = distinct !DISubprogram(name: "setindex!;", linkageName: "setindex!", scope: !57, file: !57, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!81 = !DILocation(line: 45, scope: !41, inlinedAt: !82)
!82 = !DILocation(line: 102, scope: !44, inlinedAt: !46)
!83 = !DILocation(line: 86, scope: !84, inlinedAt: !86)
!84 = distinct !DISubprogram(name: "-;", linkageName: "-", scope: !85, file: !85, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !2, retainedNodes: !38)
!85 = !DIFile(filename: "int.jl", directory: ".")
!86 = !DILocation(line: 103, scope: !44, inlinedAt: !46)
!87 = !DILocation(line: 146, scope: !74, inlinedAt: !88)
!88 = !DILocation(line: 42, scope: !76, inlinedAt: !89)
!89 = !DILocation(line: 1419, scope: !78, inlinedAt: !90)
!90 = !DILocation(line: 1389, scope: !80, inlinedAt: !46)
!91 = !DILocation(line: 70, scope: !35)
!92 = distinct !DISubprogram(name: "pi_kernel", linkageName: "julia_pi_kernel_5874", scope: null, file: !48, line: 21, type: !37, scopeLine: 21, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!93 = !DILocation(line: 88, scope: !94, inlinedAt: !95)
!94 = distinct !DISubprogram(name: "*;", linkageName: "*", scope: !85, file: !85, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!95 = !DILocation(line: 23, scope: !92)
!96 = !DILocation(line: 513, scope: !97, inlinedAt: !98)
!97 = distinct !DISubprogram(name: "<;", linkageName: "<", scope: !85, file: !85, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!98 = !DILocation(line: 376, scope: !99, inlinedAt: !101)
!99 = distinct !DISubprogram(name: ">;", linkageName: ">", scope: !100, file: !100, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!100 = !DIFile(filename: "operators.jl", directory: ".")
!101 = !DILocation(line: 343, scope: !102, inlinedAt: !104)
!102 = distinct !DISubprogram(name: "steprange_last;", linkageName: "steprange_last", scope: !103, file: !103, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!103 = !DIFile(filename: "range.jl", directory: ".")
!104 = !DILocation(line: 325, scope: !105, inlinedAt: !106)
!105 = distinct !DISubprogram(name: "StepRange;", linkageName: "StepRange", scope: !103, file: !103, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!106 = !DILocation(line: 379, scope: !105, inlinedAt: !107)
!107 = !DILocation(line: 24, scope: !108, inlinedAt: !109)
!108 = distinct !DISubprogram(name: "_colon;", linkageName: "_colon", scope: !103, file: !103, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!109 = !DILocation(line: 22, scope: !110, inlinedAt: !95)
!110 = distinct !DISubprogram(name: "Colon;", linkageName: "Colon", scope: !103, file: !103, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!111 = !DILocation(line: 38, scope: !112, inlinedAt: !114)
!112 = distinct !DISubprogram(name: "&;", linkageName: "&", scope: !113, file: !113, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!113 = !DIFile(filename: "bool.jl", directory: ".")
!114 = !DILocation(line: 669, scope: !115, inlinedAt: !116)
!115 = distinct !DISubprogram(name: "isempty;", linkageName: "isempty", scope: !103, file: !103, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!116 = !DILocation(line: 897, scope: !117, inlinedAt: !95)
!117 = distinct !DISubprogram(name: "iterate;", linkageName: "iterate", scope: !103, file: !103, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!118 = !DILocation(line: 165, scope: !119, inlinedAt: !121)
!119 = distinct !DISubprogram(name: "Float32;", linkageName: "Float32", scope: !120, file: !120, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!120 = !DIFile(filename: "float.jl", directory: ".")
!121 = !DILocation(line: 7, scope: !122, inlinedAt: !124)
!122 = distinct !DISubprogram(name: "convert;", linkageName: "convert", scope: !123, file: !123, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!123 = !DIFile(filename: "number.jl", directory: ".")
!124 = !DILocation(line: 370, scope: !125, inlinedAt: !127)
!125 = distinct !DISubprogram(name: "_promote;", linkageName: "_promote", scope: !126, file: !126, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!126 = !DIFile(filename: "promotion.jl", directory: ".")
!127 = !DILocation(line: 393, scope: !128, inlinedAt: !129)
!128 = distinct !DISubprogram(name: "promote;", linkageName: "promote", scope: !126, file: !126, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!129 = !DILocation(line: 422, scope: !130, inlinedAt: !131)
!130 = distinct !DISubprogram(name: "+;", linkageName: "+", scope: !126, file: !126, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!131 = !DILocation(line: 25, scope: !92)
!132 = !DILocation(line: 410, scope: !133, inlinedAt: !131)
!133 = distinct !DISubprogram(name: "-;", linkageName: "-", scope: !120, file: !120, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!134 = !DILocation(line: 411, scope: !135, inlinedAt: !131)
!135 = distinct !DISubprogram(name: "*;", linkageName: "*", scope: !120, file: !120, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!136 = !DILocation(line: 411, scope: !135, inlinedAt: !137)
!137 = !DILocation(line: 332, scope: !138, inlinedAt: !140)
!138 = distinct !DISubprogram(name: "literal_pow;", linkageName: "literal_pow", scope: !139, file: !139, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!139 = !DIFile(filename: "intfuncs.jl", directory: ".")
!140 = !DILocation(line: 26, scope: !92)
!141 = !DILocation(line: 409, scope: !142, inlinedAt: !143)
!142 = distinct !DISubprogram(name: "+;", linkageName: "+", scope: !120, file: !120, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!143 = !DILocation(line: 422, scope: !130, inlinedAt: !140)
!144 = !DILocation(line: 412, scope: !145, inlinedAt: !146)
!145 = distinct !DISubprogram(name: "/;", linkageName: "/", scope: !120, file: !120, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!146 = !DILocation(line: 425, scope: !147, inlinedAt: !140)
!147 = distinct !DISubprogram(name: "/;", linkageName: "/", scope: !126, file: !126, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!148 = !DILocation(line: 409, scope: !142, inlinedAt: !140)
!149 = !DILocation(line: 521, scope: !150, inlinedAt: !151)
!150 = distinct !DISubprogram(name: "==;", linkageName: "==", scope: !126, file: !126, type: !37, spFlags: DISPFlagDefinition | DISPFlagOptimized, unit: !4, retainedNodes: !38)
!151 = !DILocation(line: 901, scope: !117, inlinedAt: !152)
!152 = !DILocation(line: 28, scope: !92)
!153 = !DILocation(line: 29, scope: !92)
Conclusions 🎉

Conclusions

2023-09-07 14 39 07

What was achieved?

We developed the first (to our knowledge) third-party programming model for the IPU with a language not officially supported by Graphcore. This was made possible by the ubiquitous LLVM compiler framework
Julia allowed us doing general-purpose programming on the IPU with a high-level language (although while still using low-level Poplar functionalities), outside of the machine learning niche
Proposed non-trivial programs using third-party packages (e.g. differential equations solver and zero-runtime-cost autodiff with Enzyme), showcasing possibility of code reuse, much larger than what can be achieved in C++
Thanks to Julia's introspection and metaprogramming capabilities we were able to simplify some aspects of writing IPU programs
We can use both single and half precision floating point numbers, including stochastic rounding for the latter
First use of Graphcore's LLVM fork
Overall, we were not concerned about performance throughout this project, the main goal being to make the basic interface between Julia and the IPU work. However, we showed that at least in the specific example of the π program performance of the LLVM IR generated by Julia (for the host CPU!) was competitive with a native C++ codelet.

Limitations and possible future work

There are many limitations for the reuse of Julia code on the IPU (no runtime: no compilation, no garbage collection, etc; no external binary libraries), but these aren't specific to IPU, in common with other offloading techniques, like GPU
Julia doesn't have native support for 8-bit floating point numbers
Only a subset of Poplar/Poplibs libraries have been wrapped
We're currently using a light C++ shim to define a vertex ➡ fully define codelet in LLVM IR
Targeting Colossus backend is very experimental (sometimes optimisation passes optimise too much) ➡ iron out integration with Colossus backend
Couldn't figure out a way to integrate with GPUArrays.jl ➡ explore other programming models (KernelAbstracts.jl, GPUArrays.jl?)
Currently no access to tile-level multi-threading ➡ is it possible to express tile-level multi-threading?

Give it a try in the cloud

Head to https://github.com/JuliaIPU/JuliaIpuDemo and follow the instructions in the README.md for how to play with Julia on the IPU in the cloud with Paperspace for free.

Julia

Code demonstration on IPU

Acknowledgements

The work of integrating Julia and the IPU was originally started by Emily Dietrich and Luk Burchard at Simula, I recently picked it up and expanded it.

My work was funded by UCL Centre for Advanced Research Computing. I'd like to thank my colleague Sofía Miñano for fruitful discussions.

I'd also like to thank developers and users of GPUCompiler.jl (Valentin Churavy, Tim "maleadt" Besard, Gabriel Baraldi, Valentin "Sukera" Bogad) for their patience in answering my questions, and Graphcore engineers (Mark Pupilli, Andrew Fitzgibbon, Dave Bozier) for their support along the way, and Simula eX³ for the use of their facilities.