Training Neural Networks in Low-Dimensional Random Bases

Graphcore Research is exploring novel ways to train neural networks that could allow us to scale to substantially larger models in future.

Scaling up deep neural networks can significantly improve model performance and this has fuelled massive growth in the number of parameters in state-of-the-art architectures. Many of today’s leading innovators in machine intelligence are pushing the boundaries of large-scale optimisation with increasingly large models. For Graphcore customers who are looking to run large and complex models across IPU-POD systems, enabling model efficiency at supercomputing scale is a key priority, since this results in high performance while reducing the cost of compute.

Stochastic Gradient Descent (SGD) has proven to be remarkably effective for the optimisation of modern large-scale neural networks. However, SGD computes the gradient with respect to every dimension of the weight space at every step, making optimisation increasingly demanding as the network size grows. The trend towards increasing model sizes therefore opens up new opportunities to improve training efficiency.

Notably, empirical evidence suggests that not all of the gradient directions of the network are required to sustain effective optimisation. Many methods are able to greatly reduce model redundancy while achieving high task performance at a lower computational cost. This includes approaches for gradient compression, weight reduction methods such as low rank projections and factorisations, as well as algorithms for sparse training.

In a new NeurIPS paper, Graphcore Research revisits a simple approach to reduce the effective network dimensionality using random projections. We leverage the hardware-accelerated random number generation of Graphcore's Intelligence Processing Unit (IPU) to train in randomly selected directions of the weight space. We show that while random projections have computational benefits, such as easy distribution on many workers, they become less efficient with growing projection dimensionality or when the subspace projection is fixed throughout training. We observe that applying smaller independent random projections to different parts of the network and re-drawing them at every step significantly improves the obtained accuracy.

Training in resampled subspaces

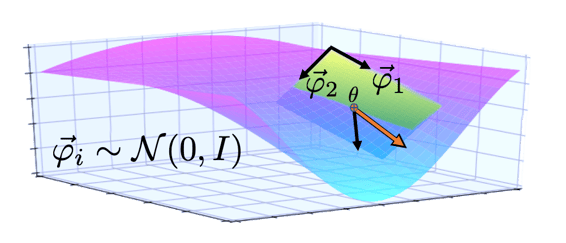
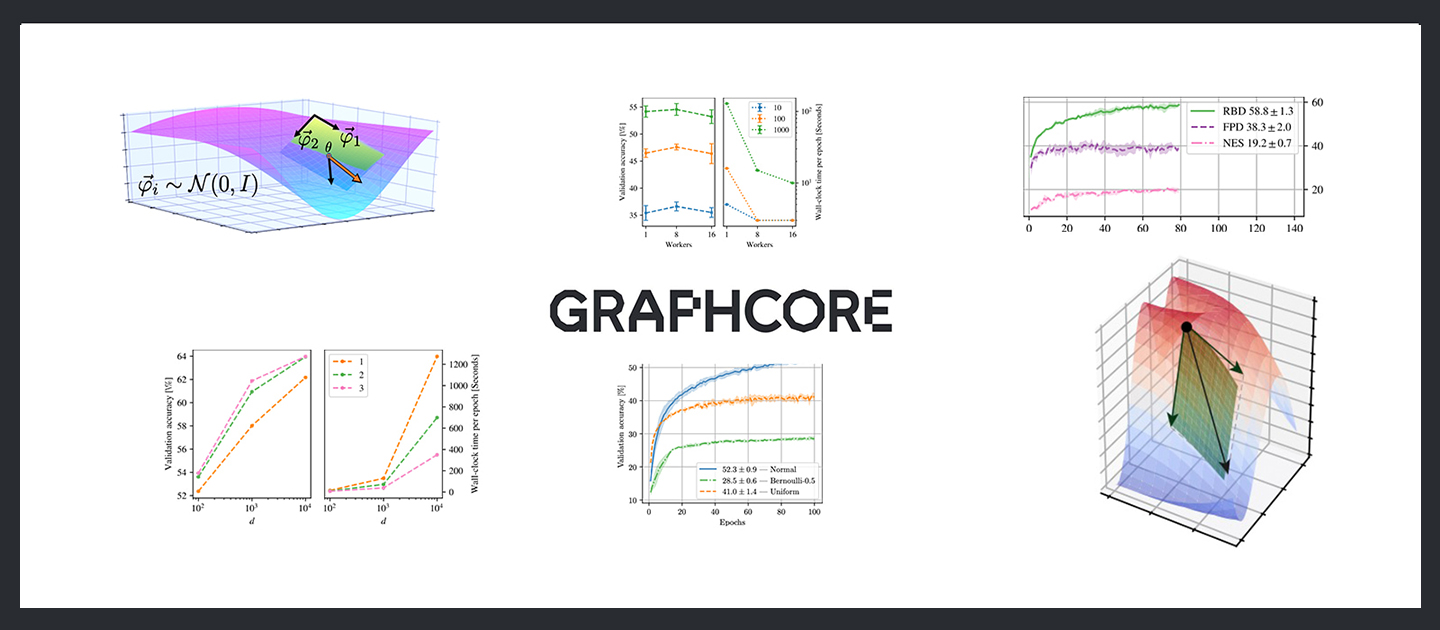
Figure 1: Schematic illustration of random subspace optimisation on a 3D loss landscape. At the point Θ, the black arrow represents the direction of steepest descent computed by conventional SGD. The coloured arrow represents the direction of steepest descent under the constraint of being in the chosen lower dimensional random subspace (the green plane).

Recent work has utilised random projections to reduce the dimensionality of neural networks (Fixed Projection Descent, FPD, Li et al., 2018). If the network weights are projected into a fixed low-dimensional random subspace, the number of trainable parameters is significantly reduced. While such training is promising for the development of more efficient and scalable optimisation schemes, its practical application is limited by inferior optimisation performance.

One issue with training in a fixed subspace is that the optimisation progress is constrained to a particular random projection that cannot evolve over the course of the training. Resampling the subspace during training, however, is challenging on conventional hardware, since generating, storing, and fetching many different projections is computationally demanding. For example, training a ResNet architecture in a subspace that spans 1% of the available dimensions and is resampled at every step for 100 epochs requires approximately 10 trillion random samples. While such a number of samples may be challenging for conventional hardware accelerators, Graphcore's first generation IPU can generate this number of samples in just 10 seconds. This allows us to sample the necessary random projection locally on the processor where the computation happens – substituting fast local compute for expensive communication. The full projection is never kept in memory but encoded as a sequence of random seeds. Furthermore, samples are generated on demand during the forward pass and re-generated from the same seed during the backward pass. As a result, we can experiment with resampled random projections while maintaining a high training throughput and low memory requirements, even when scaling to larger architectures.

The training can be accelerated further through parallelisation on many workers. As with SGD, training can be made data parallel, where workers compute gradients on different mini-batches and then average them. Equally, random subspace training can be parallelised by having different workers compute gradients of different random projections. Gradients can be exchanged using less communication bandwidth than SGD by communicating the low-dimensional gradient and the random seed of the projection. In practice, we observe constant training accuracy and almost linear wall-clock scaling when increasing the number of workers (Figure 2).

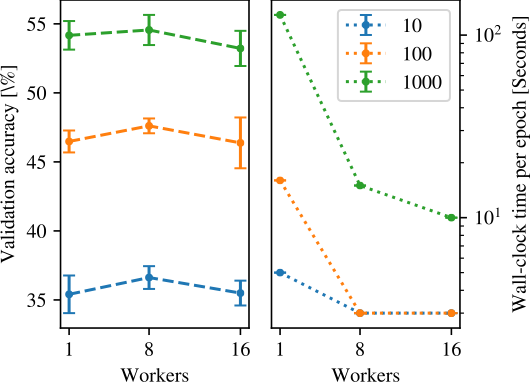
Figure 2: Investigating distributed training of our algorithm. Left: Validation accuracy is constant whether using 1, 8 or 16 workers. Right: Distributing the work leads to considerable reduction in wall-clock time for networks of varying dimensionality.

Resampling subspaces outperforms fixed hyperplanes

We find that training in a resampled random subspace of the network yields significant optimisation benefits. Re-drawing the subspace at every step (Random Bases Descent, RBD) improves the obtained accuracy on fully connected and several convolutional architectures, including ResNets on the MNIST, Fashion-MNIST and CIFAR-10 datasets (Figure 3).

Notably, our gradient based approach also clearly outperforms black-box optimisation with Evolution Strategies that require an equal number of random samples. This discrepancy demonstrates an advantage of the gradient-based subspace training in low dimensions over derivative-free optimisation.

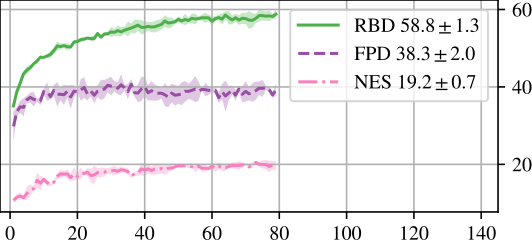
Figure 3: Validation accuracy (y) against epochs (x) for CIFAR-10 classification of a 78,330-parameter ResNet-8 using low-dimensional optimisation with d=500 dimensions. Our method RBD improves upon the same-d FPD baseline (Li et al. 2018) as well as black-box NES optimisation (Salimans et al. 2017) by 20.5% and 39.6% respectively.

Dimensionality and approximation

Intuitively, performance can be improved by increasing the size of the subspace. However, empirically we find that a linear improvement in the gradient approximation requires an exponential increase in the number of subspace directions. As a result, matching SGD performance quickly becomes computationally prohibitive.

To improve the approximation efficiency, we experiment with constraining the dimensionality by partitioning the network into smaller compartments that use independent random projections. While the overall number of gradient coefficients remains unchanged, partitioning the space constrains the dimensionality of randomisation, which can make random approximation much more efficient (Gorban et al., 2015).

To test this idea, we compare the performance of the network with differing numbers of compartments and with the network's parameters evenly split between compartments. We find benefits in both achieved accuracy and training time from this compartmentalisation scheme (Figure 4).

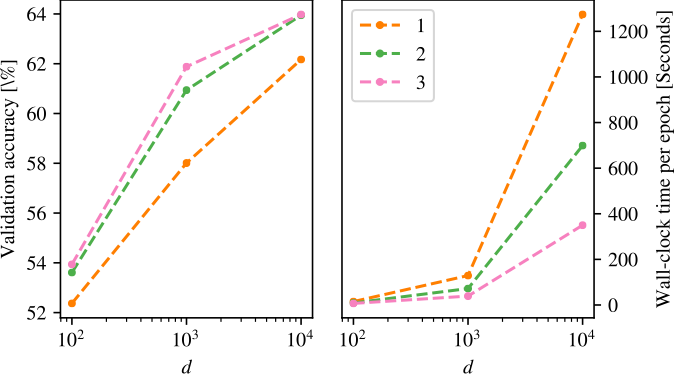
Figure 4: Investigating a compartmentalisation of random projections. Left: Validation accuracy under varying number of compartments. Right: Wall-clock time for these experiments. Compartmentalisation both increases the accuracy and improves training time.

Sampling directions matter

The effectiveness of the optimisation not only relies on the dimensionality of the random subspace, but also on the type of directions that are explored and their utility for decreasing the loss. We experiment with Gaussian, Bernoulli and Uniform distributions and find that the training performance of the Normal Distribution is superior across different network architectures and datasets (Figure 5). This suggests that an improved design of the directional sampling distribution could boost the descent efficiency and shed light on the directional properties that matter most for successful gradient descent. Many existing techniques that have been developed for randomised optimisation such as covariance matrix adaptation (Hansen, 2016) or explicit directional orthogonalisation (Choromanski et al., 2018), among others, can be considered.

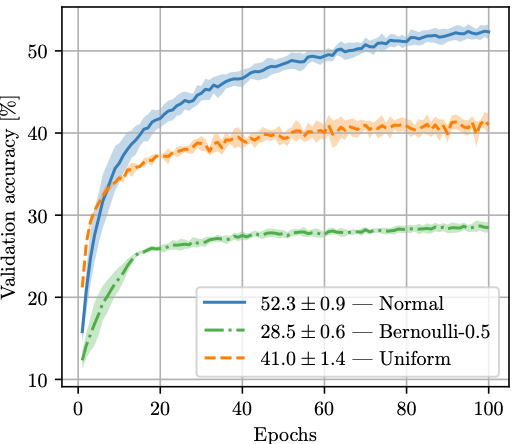
Figure 5: Validation accuracy (y) for training over 100 epochs (x) with different directional distributions Uniform in range [-1, 1], unit Gaussian, and zero-mean Bernoulli with probability p=0.5 (denoted as Bernoulli-0.5). Compared to the Gaussian baseline, the optimisation suffers under Uniform and Bernoulli distributions whose sampled directions concentrate in smaller fractions of the high-dimensional space.

Future directions for neural network optimisation

Overall, our work provides further evidence that neural networks can be optimised by exploring only a small fraction of directions of their weight space.

In future work, we aim to learn the sampling distribution of the subspace in order to generate better candidate subspaces. We also intend to explore training larger models, where the size of the subspace may match today’s “large models”.

The advent of hardware-accelerated random number generation may mean that randomised optimisation strategies are well-poised to take advantage of massively parallel compute environments for the efficient optimisation of very large-scale models.

Graphcore would be delighted to hear from other organisations engaging in similar research. Please send an email to info@graphcore.ai if you are conducting research within this field and are interested in gaining access to IPUs under our academic program. 

Read The Full Paper

Check out the TensorFlow Source Code on GitHub