What links brains, worms and parallel processors for AI?

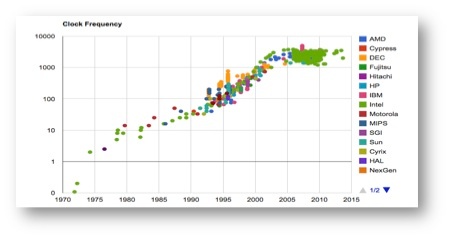
Processors are not getting faster

The scaling potential for semiconductor chips, Moore’s Law, first observed by Gordon Moore in his 1965 Electronics Magazine paper “Cramming more components onto integrated circuits”, has held true for the last 50 years, albeit with some minor modifications. Semiconductor technology is still improving and Moore’s Law logic scaling can continue for the next 10 years at least. This means we can fit more and more transistors on future processor chips.

The challenge is that the power down-scaling, which compensated for density up-scaling of semiconductor devices, as first described by Robert Dennard in 1974, no longer holds true. Dennard observed that as logic density and clock speed both rise with smaller circuits, power density can be held constant if the voltage is reduced sufficiently. But we reached the practical limit of this type of scaling around 2005, as we moved below 90nm process nodes. From that point forward it has not been practical to increase the clock speed of processors because chip power would rise too.

From the first Personal Computers built in the late 1970’s through to 2005, the industry achieved a 1,000x increase in CPU clock speed. But from 2005 onwards we have been stuck at roughly the same clock speed, around 2-3GHz. Computer designers have still been able to deliver more performance by putting down multiple processor cores. But dividing a compute workload across more than a handful of cores is tough for both hardware and software. Machine intelligence has the performance appetite for thousands or millions of collaborating processors, but new approaches to parallel computer design are required if we are to harness parallelism on such scale.

Processors are not getting faster – Source: Stanford VLSI Group

Parallel processors are hard

Putting a large number of processors down on a silicon die is not too difficult. However the real challenges are: 

• How do you get instructions and data to them?
• How do you connect them and allow them to share data?
• And how can you make a parallel machine that is simple to program?

So far one of the most commercially successful parallel machines has been the Graphics Processor Unit (GPU). GPU vendors talk in terms of “cores” to exaggerate their parallel credentials, but a GPU core is not at all the same thing as a CPU core. Modern GPUs advertised as having more than 3000 “cores” have only a few 10’s of processors. The discrepancy arises because GPUs take a huge short-cut to parallelism, by feeding each processor instruction stream to a very wide vector datapath of parallel arithmetic units. They then count arithmetic units to get a high number of “cores”, but the real number of processors (CPU cores) is the number of instruction streams.

Often GPU datapaths are 32 or 64 data elements wide and every element can only experience exactly the same instruction sequence limiting the true parallelism. GPUs were designed for graphics, of course, which is characterised by low-dimensional data-structures (usually 2D images) for which wide vectors are efficient. But wide vector processors are much less efficient for the high-dimensional data which characterizes machine intelligence.

To further simplify the GPU, communication between processors relies solely on shared memory. This is not scalable beyond a few 10’s of processors. And if wide vector processors are to be replaced with narrower processors for efficiency on machine intelligence workloads, we’ll need a lot more of those narrow processors. Even then shared memory communication isn’t going to be feasible; a direct processor-to-processor messaging interconnect is required.

GPUs also require all data to be stored in external memory, creating huge bandwidth and latency bottlenecks. GPU vendors have tried to mitigate this by adding hierarchical caches and more recently by adding expensive 3D memory devices such as High-Bandwidth Memory (HBM), requiring expensive silicon interposers with Through-Silicon-Via (TSV) connections. If a means were found to increase the raw compute performance of the GPU, then this off-chip memory bottleneck would just get proportionally worse.

Some recent processor designs targeting machine intelligence have focused on producing variations of vector machines but using lower-precision arithmetic. This offers higher compute density of course, but does not answer the external memory bottleneck.

Some companies have tried to build arrays of processors which communicate via simple north-south, east-west neighbour connections. Sometimes this pattern is combined with so-called data-flow execution, in which compute is driven by the arrival of data. The problem with all the multiple processor machines built so far is that they have completely inadequate interconnect and memory bandwidth to support true thousand- or million-way parallelism on chip. Occasionally a single benchmark can be found that shows a performance advantage but inevitably this turns out to be hand coded, relying on a very precise flow of data through the machine. More general problems turn out to be nearly impossible to program and performance is disappointing.

The key to solving this problem lies in the striking similarities I mentioned at the start, between the networking structures of human brains, the nematode worm and complex routing in logic chips.

Rentian Scaling

Magnetic Resonance Imaging data from human brains has shown us the highly complex three-dimension network of connections that exists between neurons in the brain. Mapping the corresponding “connectome” of the human brain is a work in progress.

Professor Edward Bullmore and his team at Cambridge University have studied the fractal architecture seen in the human brain, with its similar patterns repeating over and over again at different scales and noted the striking similarity to the simpler structures that have been fully mapped in the nervous system of the nematode worm Caenorhabditis Elegans. These 3-D structures are also strikingly similar to the highly complex 2-D connections seen inside complex logic circuits in semiconductor chips.

In human brains it is estimated that approximately 77% of the volume is taken up with communication. As mammalian brain size increases, the volume devoted to communication increases faster than the volume devoted to functional units and the ratio between the two is approximate to a power law. This same power law relationship between logical units and interconnect was observed in electronic circuits by E.F. Rent, a researcher at IBM back in the 1960’s. Rent found a remarkably consistent relationship between the number of input and output terminals (T) at the boundaries of a logic circuit, and the number of internal logic components (C). On a log–log plot, the data points mapped to a straight line, implying a power-law relation T = t C ^p ,where t and p, are constants (p < 1.0, generally in the range 0.5 < p < 0.8).

Any engineer familiar with designing Field Programmable Gate Arrays (FPGA) will understand the importance of interconnect vs logic units. Over 75% of the die area in an FPGA is taken up with programmable interconnect or I/O, leaving a relatively small part of the die area for programmable logic elements. FPGAs try to comply with Rent’s rule for the amount of interconnect vs. logic units at a local scale. Over small areas of the FPGA, Rentian scaling is accommodated, but over the full FPGA there is simply not enough programmable interconnect available. So when you try to fully use all the logic elements in an FPGA you typically run out of interconnect.

A parallel processor for machine intelligence (MI)

The knowledge models that we are trying to build and manipulate in machine intelligence systems are best conceived as graphs, in which vertices represent data features and edges represent correlations or causations between connected features. Such graphs expose huge parallelism in both data and computation that can be exploited by a highly parallel processor. None of the machines available today have been designed to exploit parallelism at this scale, but modern silicon technology will support it. In fact, returning to the post-Dennard world, modern silicon technology also requires this level of massive parallelism.

The key however is to carefully consider the critical issues around how we connect processing elements together and how we keep memory local to processing units. The simple approaches taken by GPUs and today’s multi-core CPUs are already both near their architectural efficiency limits. A breakthrough is required in the design of interconnect that can support Rentian scaling in large-scale parallel machines. Building a machine that can efficiently share data across 1000’s of independent parallel processing elements is the only way to create the breakthrough in performance and efficiency required to fulfil the promise of machine intelligence.

And such a breakthrough in machine design will be useless unless it can deliver easy programmability, which further adds to the architectural challenge.

We will be sharing more information about how Graphcore is solving these problems and building the world's first Intelligent Processing Unit in the coming months.  To be one of the first to receive more information, please sign up for further updates here.