This year's NeurIPS conference - being held in New Orleans - takes place amid an explosion of activity in artificial intelligence: barely a week passes without the announcement of a major new generative AI model.
Ever increasing capability, however, means growing demands on the systems used to train the technology. The resulting 'compute crunch' makes the search for efficiency in AI training ever more pressing - necessitating new techniques such as the 8-bit floating point (FP8) work being presented by Graphcore's research team at NeurIPS 2013.
Less is more
The use of 8-bit number formats in AI serves as a valuable counter-balance to spiraling compute loads, requiring less storage space, consuming less bandwidth while moving data around the system, and demanding less compute horsepower to produce - in many cases - comparable results.
By definition, 8-bit notation is able to represent far fewer values than 16-bit formats (see graphic) making it necessary to solve the problem of maintaining numerical stablility within the computation.
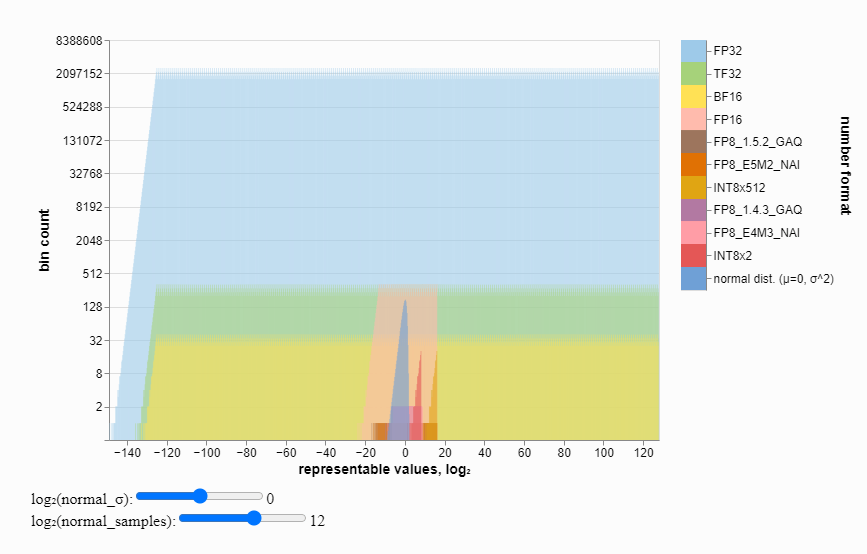
Visualising ML number formats
Our paper presents a new application of a method called FP8-AMAX which enables the computation of linear layers in Transformers models in FP8.
The main idea is to dynamically scale weights, gradients, and activations tensors individually.
This method requires enough SRAM to calculate bias locally and is particularly suited to processors such as the IPU.
In order to choose the correct scaling bias at runtime we apply the following rule:
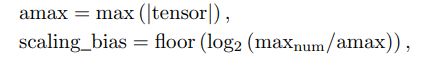
By applying it at inference time we can ensure that the model's computations stay within the addressable range of values and maintain the accuracy of the high-precision source models.
We can verify this empirically by choosing established transformer-based models and running standard benchmarks in inference mode first.
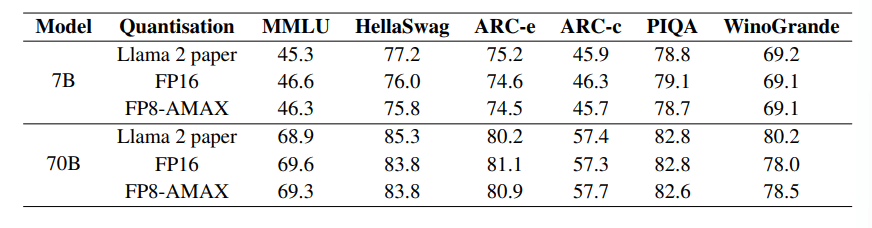
Inference results for Llama 2
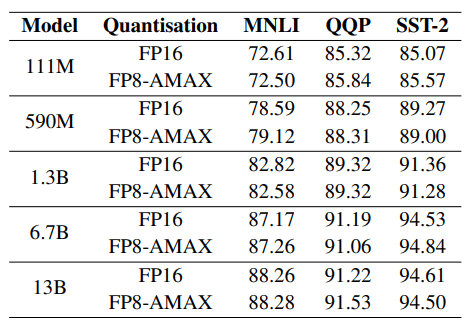
Looking at training models, we applied the same scaling rule while additionally deciding to use two different 8-bit representations.
The weights and activations are in FP8 E4 format, while the gradients use the FP8 E5 format to allow for a wider dynamic range.
Here, we validate that GPT models can be fine-tuned this way.
Low-precision numerical formats, particularly at 8-bit scale and under, are a very active research area in machine learning.
By co-developing hardware and software solutions, we envision important gains will continue to be made in the efficiency of AI computing systems.
