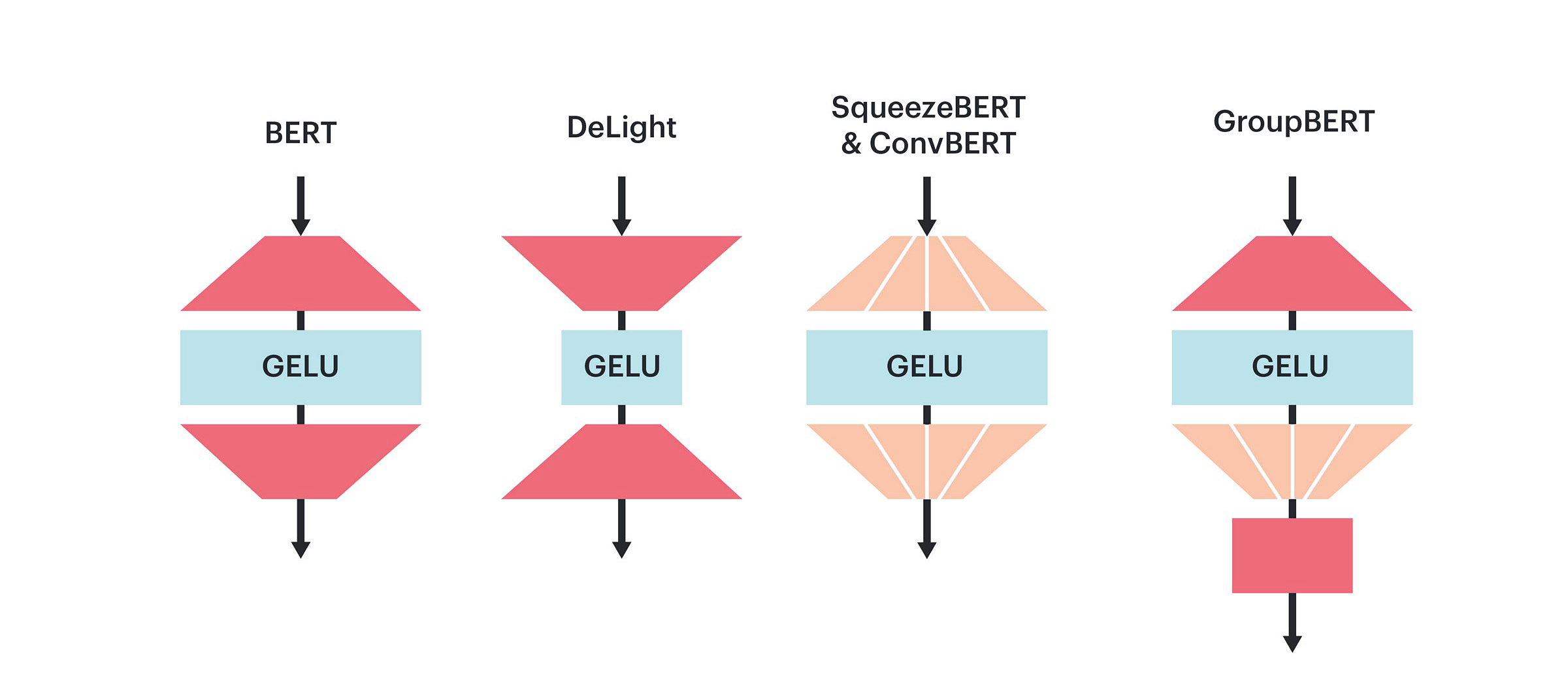
BERT has established itself as one of the most popular and versatile AI models in use today. However, BERT’s dependence on dense operations means that its accuracy and flexibility comes at a high computational cost.
In response to this challenge, Graphcore Research has developed GroupBERT, a new BERT-based model that uses grouped transformations, making it perfectly suited for our Intelligence Processing Unit (IPU).
GroupBERT combines an enhanced Transformer structure with efficient grouped convolutions and matrix multiplications, enabling IPU users to effectively halve the number of parameters in a model and reduce the training time by 50%, while retaining the same level of accuracy.
Enhanced BERT unlocked by the IPU
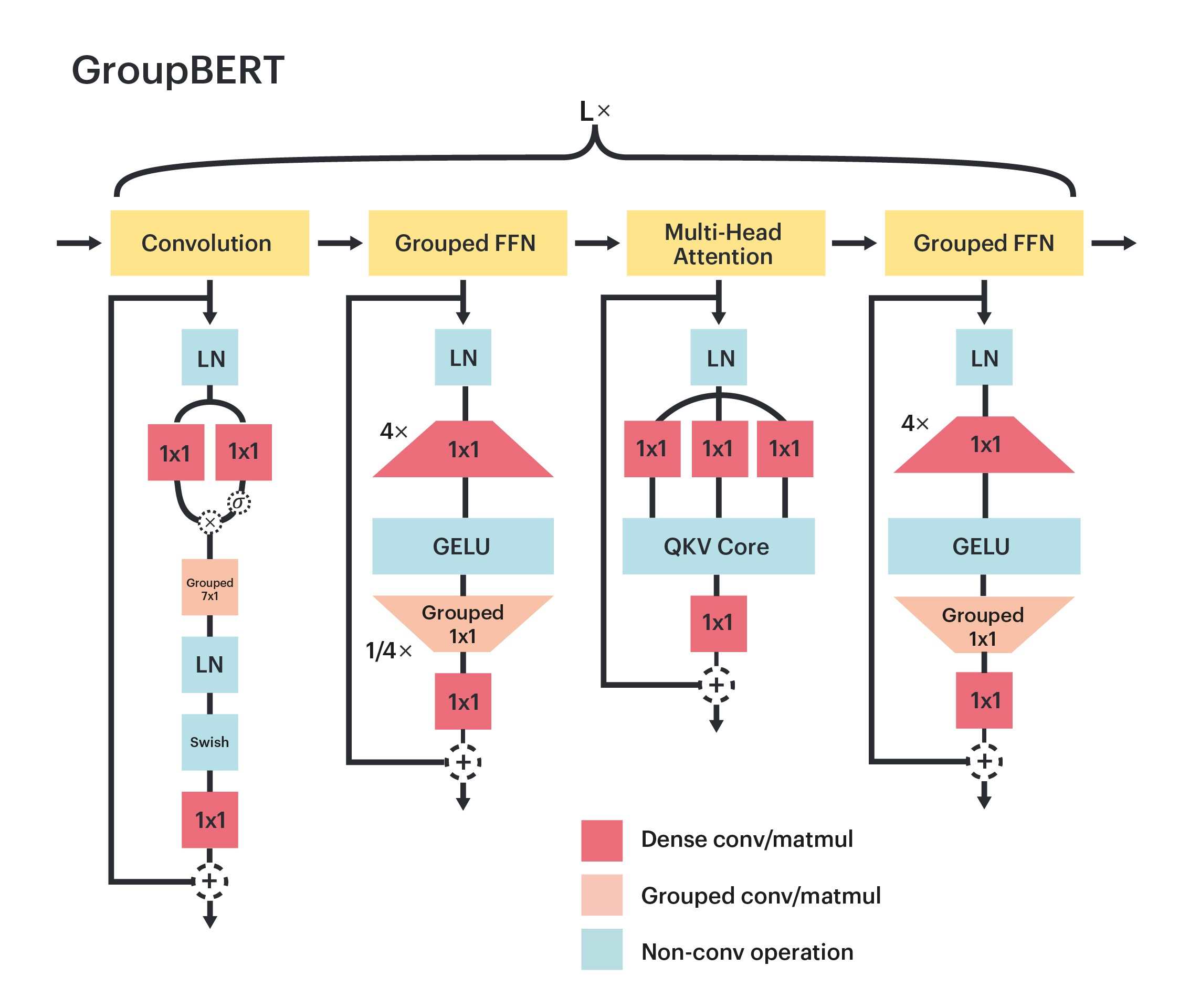
Figure 1: Schematic diagram of GroupBERT model structure.
Our paper “GroupBERT: Enhanced Transformer Architecture with Efficient Grouped Structures” [1] shows how the IPU allows Graphcore Research to explore very efficient and lightweight building blocks to derive a Transformer encoder structure that is more efficient at masked pre-training on a very large corpus of text.
GroupBERT takes advantage of grouped transformations. We augment the fully connected modules with grouped matrix multiplications and introduce a novel convolution module into the structure of the transformer. Therefore, each GroupBERT layer is extended to four modules, rather than two as in the original BERT.
With GroupBERT we see a significantly improved tradeoff of FLOPs and task performance as measured by validation loss. To reach the same loss value, GroupBERT requires less than half the FLOPs of a regular BERT model, which uses only dense operations and does not utilise its depth potential.
The increased depth and reduced arithmetic intensity [2] of the GroupBERT’s components accentuate memory access. Compared to dense operations, grouped operations perform less FLOPs for a given input activation tensor. To utilise the compute, these low arithmetic intensity operations require a faster data access than dense compute. Since the IPU allows all weights and activations to be stored in on-chip SRAM with an extremely high 47.5 TB/s bandwidth, it can translate GroupBERT’s theoretical efficiency advantage into a practical time-to-train reduction across a wide range of models.
Grouped Fully Connected Layers
The original Transformer encoder layer consists of two modules: multi-head attention (MHA) and fully connected network (FFN). Many works have focused on increasing its efficiency. Tay et al. (2020) [3] outlines a variety of different approaches, where most modifications have focused on reducing the quadratic computational dependency of the MHA module on sequence length. However, in BERT, the majority of computation is performed with a relatively moderate sequence length of 128 and the FFN module consumes by far the most resources, contributing nearly two thirds of FLOPs during model execution.
The structure of the FFN module is very simple: it consists of two matrices and a non-linearity. The first matrix projects the representation into a higher dimension, commonly four times larger than the model hidden representation. This dimension expansion operation is followed by a non-saturating activation function that performs non-linear transformation of the representation and sparsifies it. Lastly, the sparse expanded representation is contracted down to model dimension by the down-projecting matrix.
GroupBERT introduces a novel scheme that makes the FFN computation cheaper and faster. A key observation is that the sparsity induced by grouping is best applied to matrices that receive sparse inputs. Therefore, we only introduce grouped matrix multiply into the second down-projection matrix, making it block diagonal. However, grouped operations induce a locality constraint on the incoming hidden representation, limiting channel information propagation during the transformation. To resolve this issue, we mix groups together with an output projection, akin to MHA block that also partitions the hidden representation for multiple heads.
Overall, this Grouped FFN (GFFN) scheme allows GroupBERT to reduce the parameter count of the FFN layer by 25% with minimal reduction in task performance. This contrasts with all previous methods that attempted to use grouped transforms, but applied it to both matrices. This resulted in a disjoint hidden representation and causes significant performance degradation.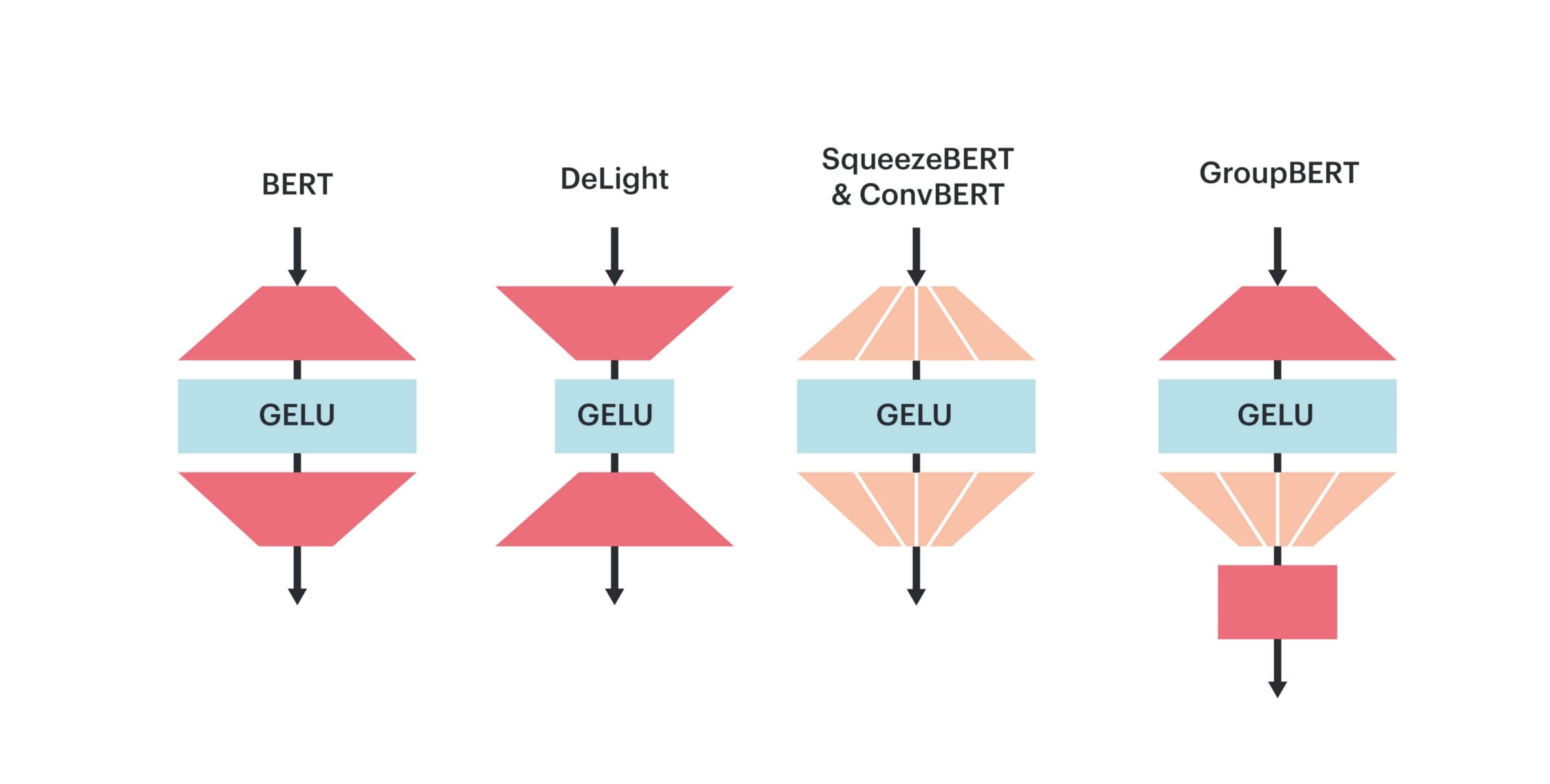
Figure 2: GFFN uses a novel scheme to apply grouped matrix multiplies that preserves performance and saves computation.
Grouped Convolution as a complement to attention
Computing an all-to-all attention for sequence lengths used in BERT does not cause significant computational overhead. However, a recent study (Cordonnier et al. 2020) [4] has shown that using only multi-head attention can be superfluous in the first place for language models. A subset of attention heads in a Transformer layer collapses into a convolutional mode to model solely local token interactions.
To alleviate the redundancy of calculating dense attention maps for modelling local interaction within a sequence, GroupBERT introduces a dedicated Convolution module. A grouped convolution acts as a sliding window, mixing information between word tokens that are close to one another. We then extend the encoder with an additional GFFN to follow the convolution module, ensuring that every token-processing module is coupled with a feature processing GFFN module.
With these additional modules, local token interactions have a dedicated lightweight model element. This in turn enables the MHA attention to perform better at modelling long-range interactions only, since less attention capacity is spent on local token interactions. Figure 3 shows attention maps from both BERT and GroupBERT over the pre-training validation set. This is a clear visualisation of how leveraging convolutions allows attention to be more efficient at long-range interactions, as the pattern is smoother and more spread out.
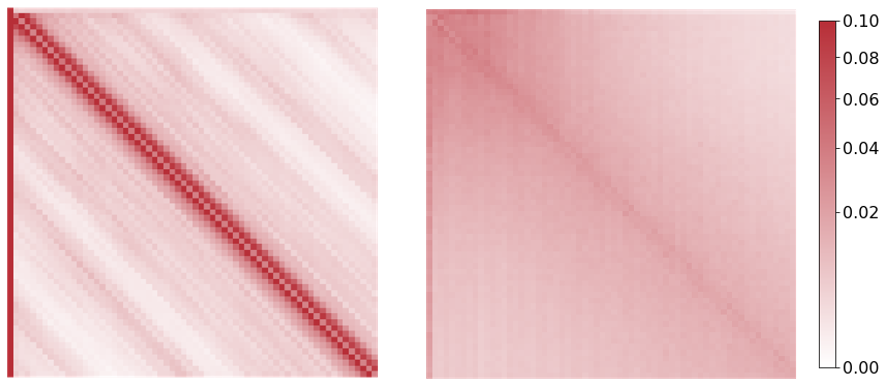
Figure 3: Attention maps generated by BERT (left) and GroupBERT (right) from the validation set data. GroupBERT attention is less dependent on relative position, enabling it to focus better on long-term interactions.
Making model parameters count
Normalisation
Many works have considered the best approach to apply normalisation in a Transformer. While Layer Normalisation is always the preferred method of normalisation, there are two variants of how it is applied: PreNorm and PostNorm.
PostNorm normalises the output of the sum of skip-connection and the residual, while PreNorm normalises the representation of the residual branch before the applying any projections within, as shown on Figure 4.

Figure 4: PostNorm (left) and PreNorm (right) position the Layer Normalisation (LN) function at different location with respect to the residual and skip connections.
The standard implementation of BERT uses PostNorm, which has a benefit of delivering stronger task performance than PreNorm under the setting when the default learning rate is used. However, we find that PreNorm configuration is significantly more stable and can use higher learning rates, that are unavailable for a PostNorm model.
GroupBERT uses PreNorm and achieves superior task performance as the model can now stably accommodate a 4x increase in learning rate compared to the PostNorm baseline which diverges at such high learning rates. Higher Learning rates are important for increasing model generalisation and achieving a better rate on convergence.
Higher learning rates do not lead to computational savings directly. However, achieving higher task performance would otherwise require a larger model, resulting in higher computational cost. Therefore, achieving higher learning rates by increasing model stability increases the efficiency of utilising model parameters.
Dropout
Many language models based on the Transformer architecture benefit from using dropout, as it reduces overfitting to the training dataset and helps generalisation. However, BERT is pre-trained on a very large dataset and in this case, overfitting is typically not an issue.
For this reason, GroupBERT removes dropout during pre-training. The FLOPs involved in multiplication of dropout masks are negligible, so it can also be considered a FLOP-neutral optimisation. However, generating dropout masks can have a significant throughput overhead, so the removal of this regularisation method in BERT is beneficial for faster model execution and better task performance.
While it is advantageous to perform pre-training on the Wikipedia dataset without dropout, dropout remains a vital tool during fine-tuning of GroupBERT, as fine-tuning datasets are several orders of magnitude smaller than the pre-training corpus.
GroupBERT: an IPU transformer
Before combining all of the outlined modifications together in a single model, we have to verify the effectiveness of each component. However, grouped FFNs reduce the number of model FLOPs, while adding a convolution module increases the FLOPs. For this reason, comparing directly against BERT is unfair as models can consume a different amount of resources. To determine the quality of our model enhancements of various sizes, we have to compare them to a logarithmic interpolation between BERT models of different sizes: Medium, Base, and Large.
Figure 5 presents an fragmentary ablation study of each enhancement introduced to GroupBERT. Every addition to the model increases Pareto efficiency compared to baseline BERT. When combined, GroupBERT Base achieves the same MLM validation loss as BERT Large model, even though it has less than 50% of the parameters.
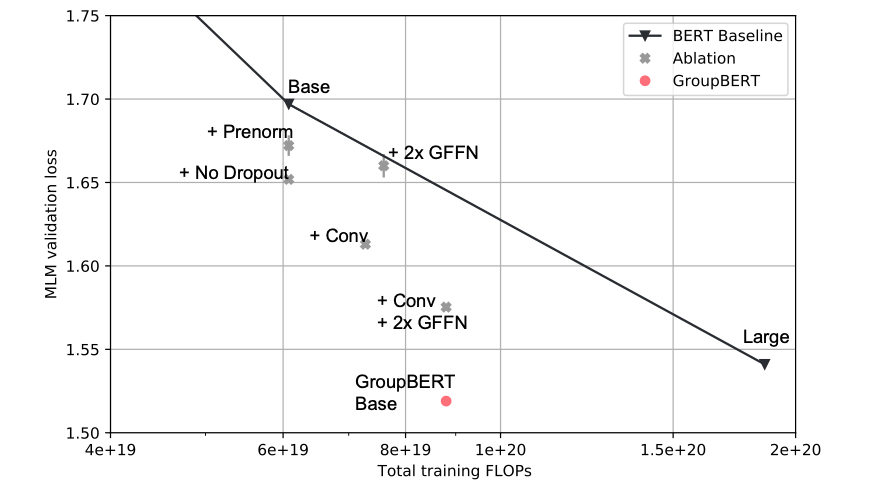
Figure 5: GroupBERT Ablation study. All enhancements introduced in GroupBERT increase Pareto efficiency of BERT as they achieve a lower validation MLM loss. Image by author.
To definitively conclude that GroupBERT is superior to BERT, we show that the advantage of GroupBERT Base over BERT Large persists over a wide range of model scales. We complement GroupBERT Base model with two additional model sizes to create a continuous Pareto front. This approach, visualised on Figure 6, enables us to show a constant advantage of GroupBERT over BERT, as well as other proposed models that attempt to use grouped transforms in a Transformer.
.png?width=497&name=Graph%20(2).png)
Figure 6: Pre-training validation accuracy against FLOPs.
With GroupBERT being an IPU-native model, the theoretical savings achieved in terms of FLOPs also translate to better end-to-end pre-training time required to reach a given level of validation accuracy.
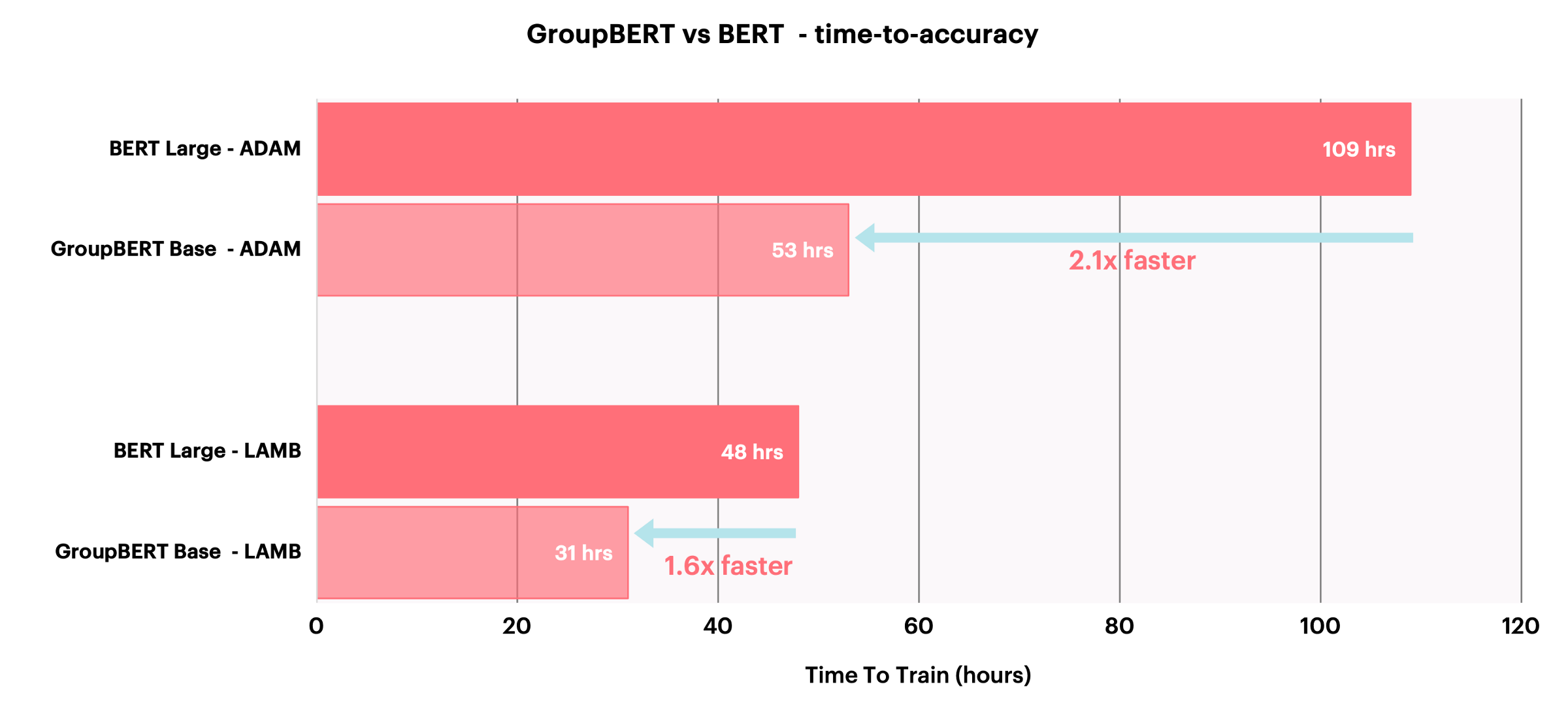
Figure 7: Training times of GroupBERT Base vs BERT Large for different optimisers on IPU-POD16. All models reach equivalent pre-training validation accuracy.
Key Takeaways
Our results show that:
- Grouped transformations can create much more efficient models
- Combining convolutions with dense all-to-all attention has a beneficial impact even for tasks that require long-range interactions
- IPU translates theoretical FLOP savings to practical savings in computation time
- Significant performance gains can be achieved with architectural changes, rather than simple model scaling
In summary, GroupBERT can achieve up to 2x improvement over original BERT in terms of pre-training performance, enabling faster and more efficient computation.
Read the Paper
Access the Code on GitHub
Thank you
Thank you to Daniel Justus, Douglas Orr, Anastasia Dietrich, Frithjof Gressmann, Alexandros Koliousis, Carlo Luschi and David Svantesson who also contributed to this research, and thank you to our other colleagues at Graphcore for their support and insights.
References
[1] I. Chelombiev, D. Justus, D. Orr, A. Dietrich, F. Gressmann, A. Koliousis, C. Luschi, GroupBERT: Enhanced Transformer Architecture with Efficient Grouped Structures (2021), arXiv
[2] D. Masters, Delving Deep into Modern Computer Vision Models (2020), graphcore.ai
[3] Y. Tay, M. Dehghani, D. Bahri, D. Metzler, Efficient Transformers: A Survey (2020), arXiv
[4] J.B. Cordonnier, A. Loukas, M. Jaggi, On the Relationship between Self-Attention and Convolutional Layers (2020), arXiv