Graphcore Research has published a new paper examining three methods for optimising computer vision model EfficientNet’s performance on Intelligence Processing Units (IPUs). By combining all three techniques, we achieve a 7x improvement in throughput for training and more than 3.6x for inference.
Optimising EfficientNet for Practical Applications
In our new paper “Making EfficientNet More Efficient: Exploring Batch-Independent Normalization, Group Convolutions and Reduced Resolution Training”, we take the state-of-the-art model EfficientNet, which was optimised to be – theoretically – efficient, and look at three ways to make it more efficient in practice on IPUs.
For example, adding group convolutions, which have been shown to perform extremely well on IPUs, achieved up to a 3x improvement in practical training throughput with minimal difference in the theoretical compute cost.
Combining all three methods investigated, we achieve up to a 7x improvement in training throughput and 3.6x improvement on inference on IPUs, for comparable validation accuracy.
The theoretical cost of model training, typically measured in FLOPs, is easy to calculate and agnostic to the hardware and software stack being used. These characteristics make it an appealing, complexity measure that has become a key driver in the search for more efficient deep learning models.
In reality, however, there has been a significant disparity between this theoretical measure of the training cost and the cost in practice. This is because a simple FLOP count does not take into account many other important factors, such as the structure of the compute and data movement.
Introducing Group Convolutions
The first method we investigate is how to improve the performance associated with depthwise convolutions (in other words, group convolutions with group size 1). EfficientNet natively uses depthwise convolutions for all spatial convolution operations. They are well known for being FLOP and parameter efficient and so have been successfully utilised in many state-of-the-art convolutional neural networks (CNNs). However, they present several challenges for acceleration in practice.
For example, as each spatial kernel is considered in isolation, the length of the resulting dot product operations, that are typically accelerated by vector multiply-accumulate hardware, is limited. This means this hardware cannot always be fully utilised, resulting in “wasted” cycles.
Depthwise convolutions also have very low arithmetic intensity as they require a significant amount of data transfer relative to the number of FLOPs performed, meaning memory access speed is an important factor. While this can limit throughput on alternative hardware, the IPU’s In-Processor Memory architecture delivers extremely high-bandwidth memory access which significantly improves performance for low arithmetic intensity operations like these.
Finally, depthwise convolutions have been found to be most effective when they are sandwiched between two dense pointwise “projection” convolutions to form an MBConv block. These pointwise convolutions increase and decrease the dimensionality of the activations by an “expansion factor” of 6 around the spatial depthwise convolution. While this expansion leads to good task performance, it also creates very large activation tensors, which can dominate memory requirements and, ultimately, limit the maximum batch size that can be used.
To address these three issues, we make a simple but significant alteration to the MBConv block. We increase the size of the convolution groups from 1 to 16; this leads to better IPU hardware utilisation. Then, to compensate for the increase in FLOPs and parameters, and address the memory issues, we reduce the expansion ratio to 4. This leads to a more memory efficient and computationally compact version of EfficientNet that we refer to as G16-EfficientNet.
While these alterations were primarily motivated by throughput improvements, we also found that they enabled us to achieve higher ImageNet validation accuracy than the vanilla group size 1 (G1-EfficientNet) baseline across all the model sizes. This modification leads to significant improvements in practical efficiency.
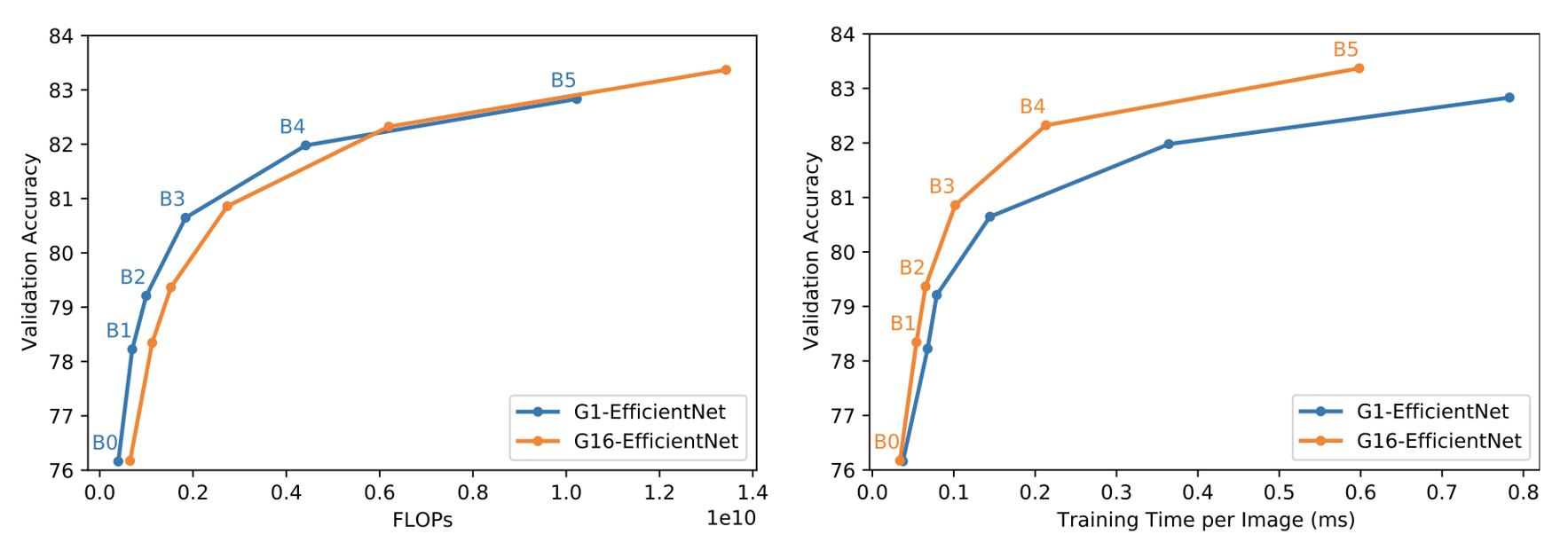
Comparison of theoretical (left) and practical (right) efficiency of G1-EfficientNet (baseline) vs G16 variant (ours)
Proxy Normalised Activations
Normalising the outputs of convolution and matrix multiply operations has become an essential element of modern CNNs, with Batch Normalisation the most common form method used for this purpose. However, the constraints on batch size introduced by Batch Norm are a well-known issue that sparked a string of innovations in batch-independent alternatives. While many of these methods work well with ResNet models, we found that none of them achieve the same performance as Batch Norm for EfficientNet.
To address this lack of alternative to Batch Norm, we leverage the novel batch-independent normalisation method Proxy Norm, introduced in a recent paper. This method builds on the already successful methods of Group (and Layer) Normalisation.
Group Norm and Layer Norm suffer from an issue where the activations can become channelwise denormalised. This issue becomes worse with depth since the denormalisation gets accentuated at every layer. While this issue could be avoided by simply reducing the size of groups in Group Norm, such a reduction in the size of groups would, however, alter the expressivity and penalise performance.
Proxy Norm provides a better fix by preserving expressivity while counteracting the two main sources of denormalisation: the affine transformation and the activation function that follow Group Norm or Layer Norm. Concretely, the denormalisation is counteracted by assimilating the outputs of Group Norm or Layer Norm to a Gaussian “proxy” variable and by applying the same affine transformation and the same activation function to this proxy variable. The statistics of the denormalised proxy variable are then used to correct the expected distributional shift in the real activations.
Proxy Norm allows us to maximise the group size (i.e. use Layer Norm) and to preserve expressivity without the issue of channel-wise denormalisation.
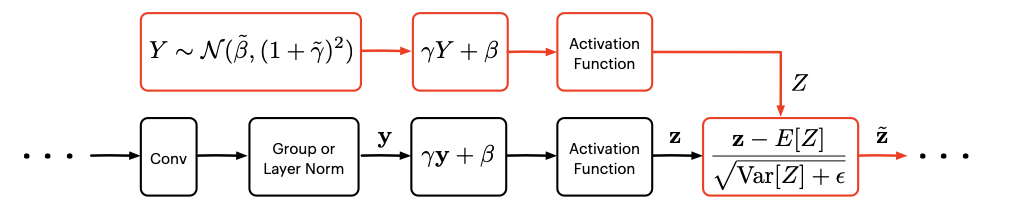
Convolution block with additional Proxy-Normalised Activation operations shown in red.
This novel normalisation technique is explored in detail in the associated paper.
Importantly, this overall approach does not emulate any of the implicit regularisation characteristics of Batch Norm. For this reason, additional regularisation is required – in this work we use a combination of mixup and cutmix. When comparing the performance of Layer Norm + Proxy Norm (LN+PN) to two Batch Norm (BN) baselines with standard pre-processing and AutoAugment (AA), we find that LN+PN matches or exceeds the performance of BN with standard pre-processing across the full range of model sizes. Furthermore, LN+PN is nearly as good as BN with AA, despite AA requiring an expensive process of “training” the augmentation parameters.
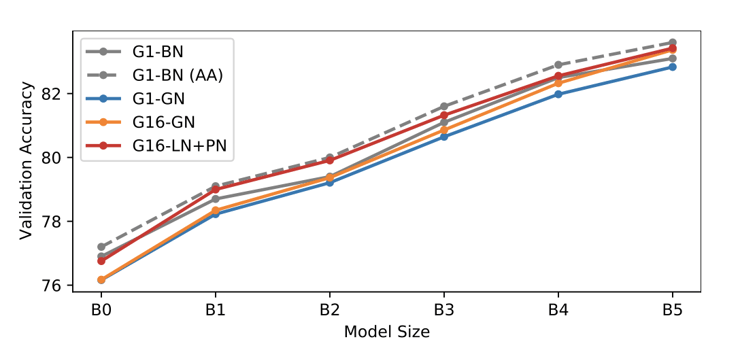
Comparison of different normalisation methods for varying sizes of EfficientNet
Reduced Resolution Training
Touvron et al. (2020) showed that significant accuracy gains could be achieved via a post-training fine-tuning of the last few layers using larger images than originally trained on. As this fine-tuning stage is very cheap, it was clear that this would achieve some practical training efficiency benefits. This raised a number of further interesting research questions. How should the training resolution be chosen to maximise efficiency? Given that larger images are slower to test on, how does this impact efficiency at inference?
To investigate these questions, we compared training at two different resolutions, either the “native” resolution (as defined in the original EfficientNet work) or at approximately half the pixel count. We then fine-tuned and tested at a broad range of image sizes. This allowed us to investigate the direct effect of training resolution on efficiency and determine the Pareto optimal combinations that achieved the best speed-accuracy trade-offs for training and inference.
When comparing training efficiency, we considered two testing scenarios: testing on the Native resolution or selecting the “best” resolution to maximise validation accuracy across the full sweep of resolutions.
When testing at the native resolution, we see that training with half-size images yields considerable theoretical and practical efficiency improvements. Remarkably, for a given model size, we find that training at half resolution and fine-tuning at the native resolution even yields higher final accuracy than training, fine-tuning and testing all at the native resolution. This conclusion suggests that, for ImageNet training, we should always be testing at a higher resolution than we train at. We now hope to understand if this applies to other domains too.
If we next allow ourselves to test at the “best” image resolution, we see that training at native resolution yields a significant improvement in final accuracy, narrowing the gap in the Pareto front.
It should, however, be noted that to achieve this, the “best” testing resolutions for the “native” training scheme end up being much larger than those that correspond to the half training resolution cases. This means they will be more expensive at inference time.
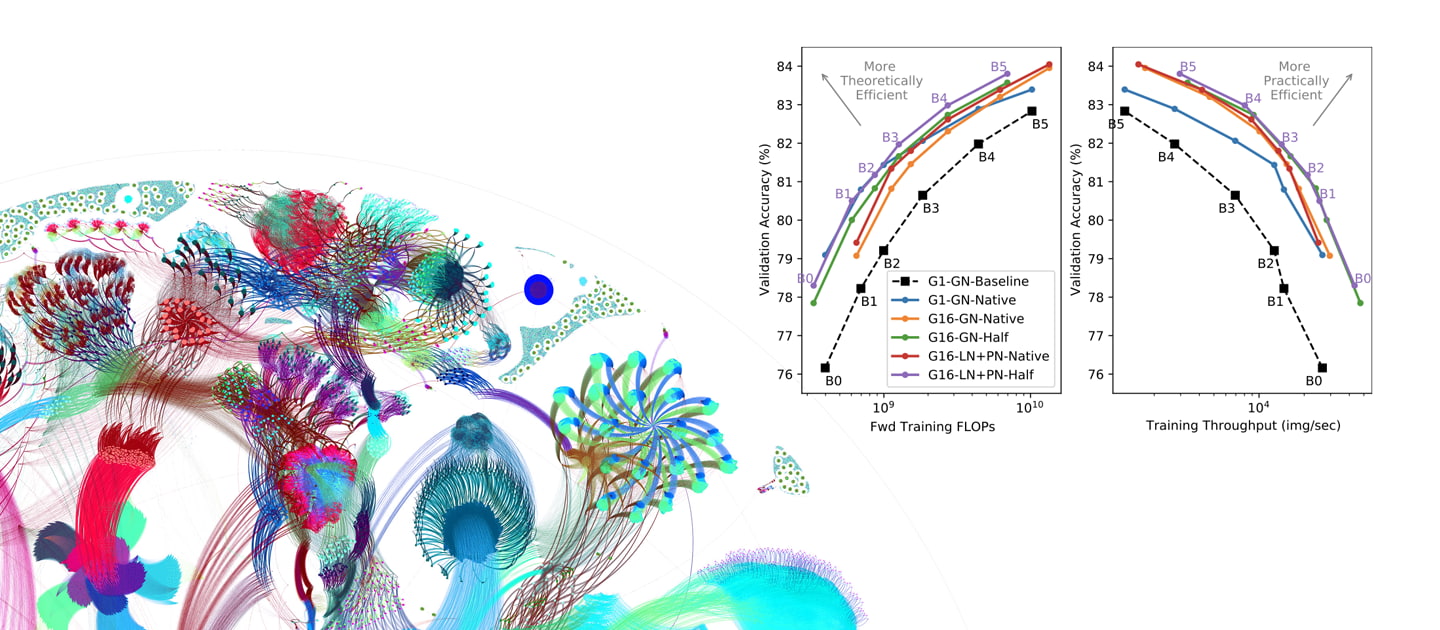
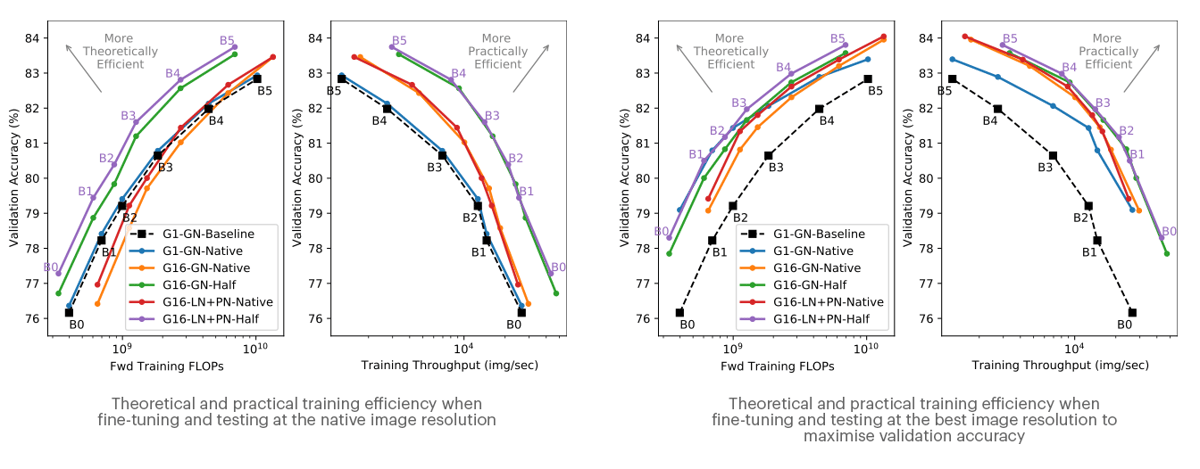 These results highlight the improvements to training efficiency achieved by the three improvements investigated (i) group convolutions [G16 (ours) vs G1]; (ii) proxy normalized activations [LN+PN (ours) vs GN] and (iii) half resolution training [Half (ours) vs Native]. Note that the baseline results have no fine-tuning and use the native image resolution.
These results highlight the improvements to training efficiency achieved by the three improvements investigated (i) group convolutions [G16 (ours) vs G1]; (ii) proxy normalized activations [LN+PN (ours) vs GN] and (iii) half resolution training [Half (ours) vs Native]. Note that the baseline results have no fine-tuning and use the native image resolution.
Comparing the efficiency of inference on its own, we see that training at half resolution yields Pareto-optimal efficiency across the full range of accuracies. This is a remarkable result as there is no direct FLOP advantage in inference at all. Furthermore, the points along the half-resolution inference-efficiency Pareto front remain optimal for training throughput.
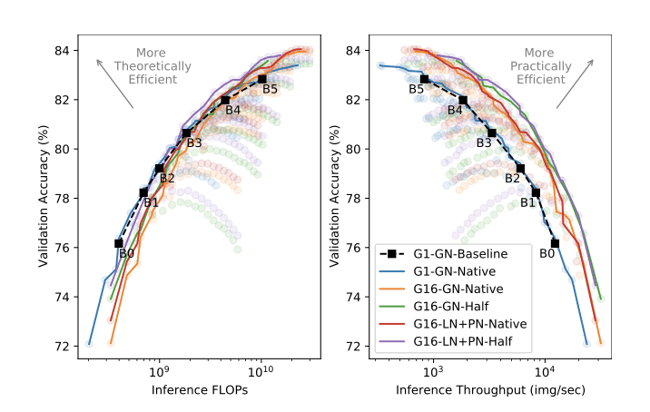
Theoretical and practical inference efficiency. Tested at all resolutions; lines highlight Pareto fronts.
Across all efficiency metrics, the models with Proxy Norm perform either equivalently to or slightly better than the models with Group Norm. This stems from the improved accuracy at only a small cost in throughput of ~10%. Importantly, however, models with Proxy Norm use fewer parameters across the whole Pareto front, highlighting an additional benefit of Proxy Norm in terms of efficiency with respect to model size.
How to make EfficientNet more efficient
In carrying out this research, we have looked at several modifications to the EfficientNet model to improve the overall efficiency in training and inference:
- By adding group convolutions and reducing the expansion ratio in the MBConv blocks, we have improved IPU hardware utilisation of the spatial convolutions and reduced the memory consumption.
- By training with images of half the resolution, we have cut training time and remarkably achieved better final accuracy.
- By leveraging the novel normalisation method Proxy Norm, we matched Batch Norm performance without any dependency on the batch information. To our knowledge, this is the first method to achieve this for EfficientNet.
Using all these methods in combination, we have achieved up to a 7x improvement in practical training efficiency and 3.6x improvement in practical inference efficiency on IPU. These results show that EfficientNet can deliver training and inference efficiency when using hardware suited to processing group convolutions, like IPU, taking it beyond the theory and towards practical, real-world applications.
This article was originally published in Towards Data Science.
Read the paper
Read the article in Towards Data Science